Trigonometria

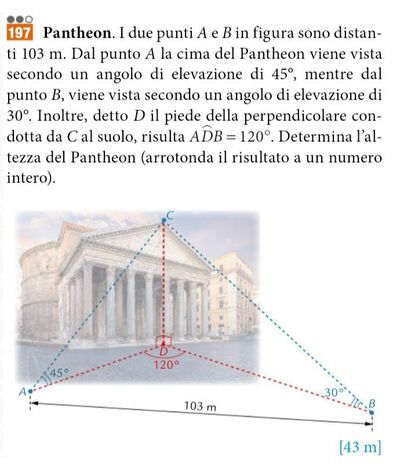
CD è l'altezza del Pantheon

CD / AD = tan45°;

CD / AD = 1;

CD = AD;  (1)

CD / BD = tan30° ;

CD = BD * radice(3) / 3;  (2)     (CD = BD * 0,577);

Eguagliamo  :  (1) = (2)

AD = BD * radice(3) / 3;

AB = 103 m;  angolo di fronte ad AB = 120° ; cos(120°) = - 0,5.

Teorema di Carnot nel triangolo ABD (a terra):

103^2 = AD^2 + BD^2 - 2 * AD * BD * cos120°;

103^2 = [BD * rad(3) /3]^2 + BD^2 - 2 * [BD * rad(3) /3] * BD * (- 0,5);

103^2   = BD^2 * 3/9  + BD^2 - 2 * BD^2 * rad(3) / 3 * (- 0,5);

103^2 = 1/3 * BD^2 + BD^2  + BD^2 * rad(3) / 3;

103^2 = [1/3 + 1 + rad(3)/3] * BD^2;

10609 = 1,911 * BD^2;

BD^2 = 10609 /1,911 = 5551,5;

BD = radicequadrata(5551,5) = 74,51 m;

AD = BD * radice(3) / 3;

AD = 74,51 * 0,577 = 43,02 m;

CD = AD;  (1);

CD = 43 metri circa, altezza del Pantheon.

Ciao @federicodonofrio

Si tratta di risolvere un sistema di tre triangoli: due rettangoli con in comune il cateto che è l'incognita principale richiesta dal problema (situazione da Teorema di Carnot); e il terzo che ha per due lati gli altri due cateti dei primi, e il terzo lato dato insieme all'angolo opposto (situazione da Teorema di Carnot).
Nomi e valori
* x = |CD|; p = |AC|; q = |AD|; r = |BC|; s = |BD|
* d = |AB| = 103 m
* α = CAD = 45°
* β = CBD = 30°
* δ = ADB = 120°
Relazioni
Il triangolo ACD è metà quadrato di lato q = x e diagonale p = x*√2.
Il triangolo BCD è metà equilatero di lato r e altezza s, quindi (x = r/2 ≡ r = 2*x) & (s = (√3)*x).
Sul triangolo ABD vale la relazione
* d^2 = q^2 + s^2 - 2*q*s*cos(δ) ≡
≡ 103^2 = x^2 + ((√3)*x)^2 - 2*x*(√3)*x*cos(120°) ≡
≡ 103^2 = x^2 + 3*x^2 - (2*(√3)*x^2)*(- 1/2) ≡
≡ x^2 = 103^2/(4 + √3) ≡
≡ x = √(103^2/(4 + √3)) = 103/√(4 + √3) ~= 43.021169 ~= 43 m