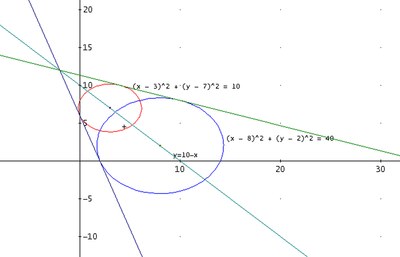
Ho due circonferenze di equazioni (x-3)^2+(y-7)^2 = 10 e (x-8)^2+(y-2)^2=40. Si intersecano in A e in B, una delle due tangenti comuni ha formula y=-3x+6. Qual è l'equazione dell'altra?
Le due circonferenze hanno centro e raggio diverso per cui una è più piccola dell'altra (escludo perciò la possibilità di tangenti parallele tra loro) il che significa che si devono per forza intersecare in un generico punto P, esterno alla circonferenza. Sarebbe facile trovare la tangente di una soltanto: calcolerei le rette passanti per P e troverei il coefficiente angolare m usando la distanza tra il fascio di rette e il centro C imponendo una distanza pari al raggio. Come posso invece garantire che la retta sia tangente ad entrambe?