[Risolto] Studio funzione

Ciao!

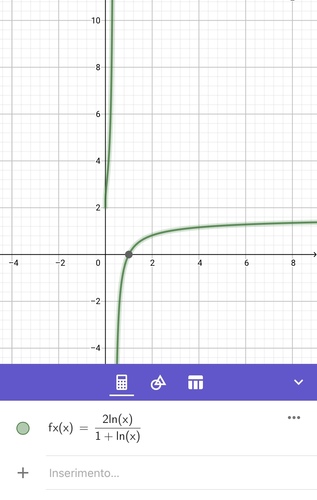
$$f(x) = \frac{2 \ln(x)}{1+\ln(x)}$$

DOMINIO: essendo una fratta, imponiamo che il denominatore  sia diverso da zero e contemporaneamente che l'argomento del logaritmo sia positivo: $\begin{cases} x > 0 \\ \ln(x) \neq -1 \end{cases} $ $\begin{cases} x > 0 \\ x \neq e^{-1} \end{cases}$ Quindi $D_f = (0 ; e^{-1}) \cup (e^{-1}; + \infty)$

PROPRIETA': non è periodica. $f(-x)$  non si può calcolare perché non si può considerare $x;0$ per via del logaritmo, quindi non può essere pari o dispari. Inoltre il dominio non è simmetrico, quindi è impossibile che sia pari o dispari. 

INTERSEZIONI: asse $x$: intersechiamo la funzione con $y = 0$: $ \frac{2 \ln(x)}{1+\ln(x)} = 0 $  $2 \ln(x) = 0 $ $\ln(x) = 0 $ $x= 1 $

Asse $y$: intersechiamo la funzione con $x = 0$: impossibile!

Perché $x=0$ non fa parte del dominio.

SEGNO: studiamo quando $f(x) > 0 $:  $ \frac{2 \ln(x)}{1+\ln(x)} > 0 $ $N: \ln(x) > 0 \Rightarrow x > 1 $ $D: 1+\ln(x) > 0 \Rightarrow x > e^{-1} $

Facendo lo studio del segno e eliminando la parte della tabella dei segni che non fa parte del dominio ricaviamo che: la funzione è $>0$ per $(0;1) \cup (e^{-1}; + \infty)$ ed è $0$ per $(1; e^{-1})$. 

LIMITI:  $\lim_{x \rightarrow 0^+} f(x) = \lim_{x \rightarrow 0^+} \frac{2 \ln(x)}{1+\ln(x)} =$ $\lim_{x \rightarrow 0^+} \frac{2 \ln(0^+)}{1+\ln(0^+)} $ che ci dà una forma di indecisione $ \frac{\infty}{\infty}$

Per risolverla possiamo usare l'Hopital: facciamo le derivate delle due funzioni separatametne: $ N': 2 \frac{1}{x}$ $D': \frac{1}{x}$ quindi: $\lim_{x \rightarrow 0^+} f(x) = \lim_{x \rightarrow 0^+} \frac{N'}{D'} = $ $\lim_{x \rightarrow 0^+} \frac{2 \frac{1}{x}}{ \frac{1}{x}} = 2 $ $\lim_{x \rightarrow (e^{-1})^-} f(x) = \lim_{x \rightarrow (e^{-1})^-} \frac{2 \ln(x)} {1+\ln(x)} = $  $\lim_{x \rightarrow (e^{-1})^-} \frac{2 \ln((e^{-1})^-)} {1+\ln((e^{-1})^-)} = \lim_{x \rightarrow (e^{-1})^-} \frac{2 \cdot (-1^-)} {1-1^-} = $  $ = \lim_{x \rightarrow (e^{-1})^-} \frac{-2} {0^-} = + \infty $ Allo stesso modo: $\lim_{x \rightarrow (e^{-1})^-} f(x) = - \infty $

Facendo il limite a $+ \infty$ ci ritroveremmo nella stessa situazione del limite a $0^+$, quindi tralascio il conto e sappiamo che fa $2$.

DISCONTINUITA': avendo già studiato i limiti sappiamo che $ x=e^{-1}$ è discontinuità di seconda specie (perché è asintoto verticale). E' l'unico punto di discontinuità perché $x = 0$ è vero che ha limite destro, ma non sinistro. DERIVATA PRIMA:  $f'(x) = \frac{ 2 \frac{1}{x} \cdot (1+\ln(x) )- (2 \ln(x))(\frac{1}{x})}{(1+\ln(x))^2} = $ $ = \frac{\frac{2+2\ln(x)-2\ln(x)}{x}}{(1+\ln(x))^2}= \frac{2}{x}\frac{1}{(1+\ln(x))^2}$ le C.E. di questa funzione sono ancora $x \neq 0$, $x_0 $, $1+\ln(x) \neq 0$ quindi non vi sono punti di non derivabilità. 

Studiamone il segno:

CRESCENZA E DECRESCENZA: $\frac{2}{x}\frac{1}{(1+\ln(x))^2} > 0 $

Il numeratore è sempre positivo, il denominatore invece:

$F_1: \ \ (1+\ln(x))^2 > 0$ per ogni $ x \in D_f$

$F_2: \ \ x > 0 $

Quindi la funzione cresce per $x > 0$ con $x \in D_f$.

Di conseguenza possiamo dire che non vi sono punti stazionari, quindi neanche massimi e minimi, flessi a tangente verticale o flessi a tangente orizzontale.

Studiamo la derivata seconda per vedere se vi sono flessi a tangenza obliqua:

DERIVATA SECONDA: deriviamola come un prodotto di funzioni

f''(x) $= (-\frac{2}{x^2})\frac{1}{(1+\ln(x))^2}+ \frac{1}{x} (-2 \frac{1}{(1+\ln(x))^3}\cdot 2(1+\ln(x) \frac{1}{x})$

$\frac{-2}{x^2(1+\ln(x))^2}- \frac{4 (1+\ln(x))}{x^2(1+\ln(x))^3} $

$ \frac{-2(1+\ln(x))-4(1+\ln(x))}{x^2(1+\ln(x))^3}$

$ \frac{-2-2\ln(x) -4-4\ln(x)}{x^2(1+\ln(x))^3} > 0 $

Per il denominatore è facile: $x ^2 > 0 $ sempre, mentre $(1+\ln(x))^3$ ha lo stesso segno di $ 1 + \ln(x)$ quindi è $>0$ per $ x > e^{-1}$

Il numeratore, invece, raccogliamo parzialmente:

$-6 \ln (x) -6 > 0 $

$ \ln (x) +1 < 0 $

$x < e^ {-1}$

Facendo lo studio dei segni per la derivata seconda vediamo che:

la derivata seconda è positiva per $ (0; e^{-1})$ e negativa per $(e^{-1}; + \infty)$. Di conseguenza nel primo intervallo la concavità sarà positiva e nel secondo intervallo sarà negativa.