Problema trigonometria

Question

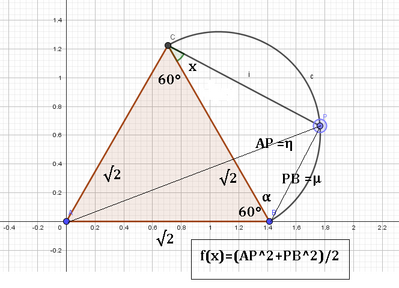
È dato il triangolo equilatero A B C di lato  sqrt {2} e la semicirconferenza di diametro C B esterna al triangolo. Sia $_a P un punto variabile sulla semicirconferenza, con P  widehat {C} B=x.a. Esprimi e rappresenta la funzione f(x)= frac { overline {A P}^2+ overline {P B}^2}{2}.b. Individua la situazione geometrica corrispondente al valore massimo della funzione.c. Discuti graficamente le soluzioni dell'equazione f(x)=k nei limiti geometrici imposti dal problem $(k  in R )$. left [ right .$ a) f(x)= frac {3}{2}+ sin (2 x- frac { pi }{6})$, con $0  leq x  leq  frac { pi }{2}; b)  max : ( frac { pi }{3} ;  frac {5}{2})$; c) $1  leq k<2$ una sol., $2  leq k  leq  frac {5}{2} due sol.].   Salve, qualcuno potrebbe gentilmente aiutarmi con questo problema?   Grazie [attach]37324[/attach]

LucianoP · Accepted Answer

Ti scrivo sino a quanto sono riuscito a fare. Poi si vedrà....

Fai riferimento al grafico in allegato. Puoi scrivere il teorema di Carnot con riferimento al triangolo APB:

η^2 = √2^2 + μ^2 - 2·√2·μ·COS(pi/3 + pi/2 - x)

η^2 = 2·√2·μ·COS(x + pi/6) + μ^2 + 2

Passa poi al triangolo rettangolo PBC:

μ = √2·SIN(x)-----> μ^2 = 2·SIN(x)^2

Quindi sostituendo hai:

η^2 = 2·√2·(√2·SIN(x))·COS(x + pi/6) + (√2·SIN(x))^2 + 2

η^2 = 4·SIN(x)·COS(x + pi/6) + 2·SIN(x)^2 + 2

hai quindi:

f(x)=(4·SIN(x)·COS(x + pi/6) + 2·SIN(x)^2 + 2 + 2·SIN(x)^2)/2

f(x)=2·SIN(x)·COS(x + pi/6) + 2·SIN(x)^2 + 1

f(x) =2·SIN(x)·(COS(x)·COS(pi/6) - SIN(x)·SIN(pi/6)) + 2·SIN(x)^2 + 1

f(x)=√3·SIN(x)·COS(x) + SIN(x)^2 + 1

che ho verificato essere identica a: f(x)=3/2 + SIN(2·x - pi/6)

Sono arrivato fin qui....

LucianoP

(@lucianop)

77299 punti

livello:

Genius II

14110 Risposte
5 7212 2874

18/02/2023 10:25

[Risolto] Problema trigonometria

Domande