Risolvi il triangolo qualsiasi $A B C$ noti i seguenti elementi:
Dati:
$$
\begin{array}{l}
A C=14,50 m \\
\alpha=C A B=67^{\circ}, 0000 \\
\beta=A B C=40,0000 \\
?_1=A B \\
?_2=B C \\
?_3=\gamma=B C A \\
?_4=\text { perimetro } A B C \\
?_5=\text { superfice } A B C
\end{array}
$$
Scusate non capisco come risolvere analiticamente il triangolo qualsiasi con le funzioni trigonometriche. Grazie.
71
punti
Livello 1
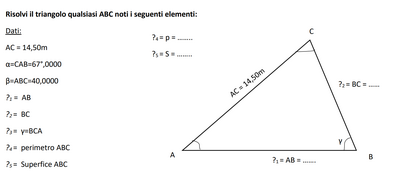
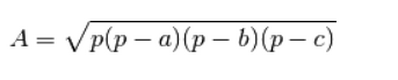Testo e disegno sono un molteplice ORRORE ("14,59m" senza ' ', "Superfice" senza 'i', "40,0000" senza '°', "γ" definito bene e disegnato a nerchia di bracco, ...).
Ricomincio da zero.
Gli angoli {α, β, γ} sono interni, rispettivamente, ai vertici {A, B, C} i cui lati opposti sono lunghi {a, b, c}.
Sono dati due angoli e un lato, non quello compreso, ma uno adiacente a un solo angolo.
* b = 14.50 = 29/2 m
* α = 67°
* β = 40°
da cui
* γ = (180 - (67 + 40))° = 73°
* a/sin(α) = b/sin(β) = c/sin(γ) = 2*R ≡
≡ a/sin(67°) = (29/2)/sin(40°) = c/sin(73°) = 2*R ≡
≡ (a = 29*sin(67°)/(2*sin(40°)) ~= 20.76) & (c = 29*sin(73°)/(2*sin(40°)) ~= 21.57) & (R = 29/(2*sin(40°)) ~= 22.56)
quindi
* p = a + b + c = (29/2)*(sin(67°)/sin(40°) + 1 + sin(73°)/sin(40°)) ~= 56.837 m
* S ~= 143.966 m^2
mi sono risparmiato tutta la dattilografia per scrivere la formula di Erone con queste espressioni.
51551
punti
Genius I
bastano un lato ed almeno due angoli di cui uno è quello opposto al lato cognito ; si applica, poi, il teorema dei seni :
a /sen α = b/sen β = c/sen Θ
96589
punti
Genius II
@remanzini_rinaldo grazie mille
Trovati i vari lati ed il perimetro come suggerito sopra, per trovare l'area viene comodo usare la formula di Erone, la quale può essere utilizzata per qualsiasi tipo di triangolo
Con $a,b,c$ misure dei tre lati e $p$ semiperimetro.
2835
punti
Livello 5
