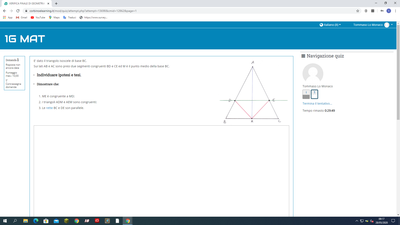
se M è punto medio di BC, allora BM è congruente a MC.
allora, considerando i triangoli MBD e MCE, si può dire che hanno due lati a 2 a 2 congruenti, ovvero BM=MC e per ipotesi BD=CE.
inoltre i due angoli compresi fra questi lati sono anch'essi congruenti fra loro, in quanto l'angolo in B è congruente all'angoli in C, poichè per ipotesi sappiamo che il triangolo ABC è isoscele.
Quindi relativamente ai triangoli MBD e MCE possiamo dire che hanno due lati conguenti e l'angolo compreso fra questi due lati anche congruente e quindi questo è sufficiente per dire che i due triangoli sono fra loro congruenti. ma se i due triangoli sono congruenti, questo significa che
DM è congruente a ME, cvd
La seconda domanda è più facile, una volta fatta la prima.
I triangoli ADM e AME hanno il lato AM a comune, quindi un lato è congruente. ma hanno anche un secondo lato congruente, in quanto dalla prima domanda sappiamo adesso che DM=ME.
per ipotesi sappiamo che AB è conguente a AC (triangoli isoscele). Allora siccome BD=CE, anche AD è congruente ad AE.
quindi abbiamo appena detto che i due triangoli ADM e AME hanno tutti e 3 i lati congruenti, quindi sono congruenti fra loro. cvd.