Ciao!
Cerco di darti un po' l'idea di come lo svolgerei io, se poi dovessi avere problemi cercherò di formalizzarlo bene domani.
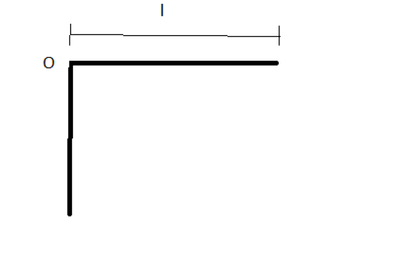
Innanzi tutto la figura: per asse orizzontale credo si intenda un asse perpendicolare al foglio (entrante o uscente, non importa il verso). Quindi il sistema presumibilmente si muoverà in verticale sotto l'azione del suo peso.
1) il momento d'inerzia rispetto ad un asse perpendicolare al piano della sbarra e passante per 0
Prima di calcolare il momento d'inerzia occorre notare che il CM non ci aiuta nell'operazione: infatti, la geometria del problema ci suggerisce che il CM sarà lungo la bisettrice dell'angolo in O, dato che questo è isoscele. Per questo motivo, direi che per il calcolo del momento d'inerzia convenga calcolare quelli che possiamo chiamare CM1 e CM2, relativi al pezzo di trave orizzontale e a quello verticale, rispettivamente.
Essi saranno esattamente a distanza $ \frac{l}{2} $ da O. Poiché il momento d'inerzia è una quantità additiva, per calcolarlo procediamo in questo modo:
1. Calcolo di $ I_{CM1} $ e $ I_{CM2} $ come $ \frac{1}{12} \frac{M}{2} l^2 $ (in quanto la trave è omogenea);
2. Calcolo di $ I_{O1} $ e $ I_{O2} $ con il teorema di Huygens-Steiner, considerando come distanza quella tra CM1 (CM2) e O;
3. Calcolo di $ I_{O} $ come somma di $ I_{O1} $ e $ I_{O2} $. (Dovrebbe tornarti $ I=\frac{Ml^2}{3} $).
2) La posizione del centro di massa rispetto ad un sistema di riferimento che ha origine in 0 e asse z perpendicolare al piano della sbarra
Questo è un problema di geometria: avendo già ragionato su dove si trova il CM, basta "dare le coordinate" rispetto ad O: sicuramente la coordinata z sarà nulla (il baricentro è nello stesso piano dell'oggetto) e giacerà sulla bisettrice del II e IV quadrante (i valori precisi si trovano con un semplice gioco di applicazione della trigonometria). (Dovrebbe tornarti $ r_{G}=(\frac{l}{4},-\frac{l}{4},0) $ ).
3) L'accelerazione angolare quando la sbarra comincia a ruotare
Ricordando che siamo in assenza di attrito, basterà ricavarla dalla formula del momento, avendo già calcolato I:
$ M=I\alpha $. A questo punto la difficoltà sta nel capire quali momenti agiscono su O: l'unico agente, sarà dato dalla forza peso sulla sbarra orizzontale, in quanto in quella verticale la forza peso ha stessa direzione del braccio, quindi non vi è momento. Il calcolo è banale, basta applicare la definizione di momento torcente (o di una forza): $ M=b\wedge F $. (Dovrebbe venirti $ \alpha=\frac{3g}{4l} $ ).
4) la componente radiale e tangenziale della reazione vincolare quando la sbarra inizia a ruotare
Questo è di certo il punto più insidioso. Ora mi perdonerai, ma non riesco a svolgermi i calcoli, né tantomeno a riportarli qui. Comunque l'idea è studiare cosa succede a livello dinamico, impostando il sistema con le tre equazioni del moto lungo le direzioni tangente, radiale e concorde con l'asse z.
Per tutte avrai espressioni del tipo: $ F_{i}+R_{i}=\frac{M}{2}a_{i} $, dove i indica la direzione (considera che lungo l'asse z non hai moto, quindi puoi subito scordarti di quest'equazione).
Ora, risolvendo il sistema tenendo conto del peso in funzione dell'angolo, ottieni che la componente della reazione vincolare lungo una data direzione è data dalla differenza tra la forza peso agente in quella direzione (quindi in funzione anche dell'angolo $ \theta $) e un termine di forza dato dalla massa per l'accelerazione lungo quella direzione, che puoi ricavare in diversi modi...uno di questi, ad esempio, è provare a ragionare sul pendolo composto (che di fatto è il sistema che consideri), e secondo me è abbastanza complicato. Un altro modo potrebbe essere ricavarsi l'accelerazione tangenziale da quella angolare e provare a giocare un po' con gli angoli.
AGGIORNAMENTO: Come ti avevo anticipato, cerco di formalizzare meglio quanto detto.
Per la reazione vincolare lungo l'asse z possiamo dire con certezza che essa risulta nulla, in quanto non agiscono forze in quella direzione.
Per quanto riguarda la direzione radiale, l'unica forza agente è la componente radiale del peso, e lungo questa direzione non avviene alcun moto; dunque, basterà scrivere:
$ R_{r}-Mgcos45 = 0 \rightarrow R_{r}=Mg\frac{\sqrt{2}}{2} $.
$ -R_{t}+Mgsin45 = Ma_{t} \rightarrow R_{t} = Mgsin45 - Ma_{t} \rightarrow $
$ R_{t} = Mgsin45 - MR\alpha \rightarrow R_{t} = Mgsin45 - M\frac{l\sqrt{2}}{4}\frac{3g}{4l} \rightarrow R_{t} = Mg\frac{\sqrt{2}}{2}(1-\frac{3}{8}) $
Quindi, in definitiva:
$ R_{t} = Mg\frac{5\sqrt{2}}{16} $
$ \vec{R} = (R_{t},R_{r},R_{z}) = Mg\frac{\sqrt{2}}{2}(\frac{5}{8},1,0) $
Spero di esserti stato d'aiuto, se domani hai dubbi dimmi e cerco di formalizzare meglio soprattutto quest'ultima parte.
Buonanotte
PS. Gentilmente, dimmi da dove hai preso questo problema, e nel caso sia un tema d'esame potresti indicarmi in che università è stato proposto?