Problema di fisica (ambito suono)

Question

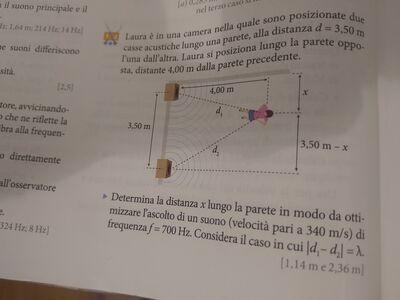
Laura è in una camera nella quale sono posizionate due casse acustiche lungo una parete, alla distanza $d=3,50 m$ l'una dall'altra. Laura si posiziona lungo la parete opposta, distante $4,00 m$ dalla parete precedente.

Determina la distanza $x$ lungo la parete in modo da ottimizzare l'ascolto di un suono (velocità pari a $340 m / s$ ) di frequenza $f=700 Hz$. Considera il caso in cui $\left|d_1-d_2\right|=\lambda$. $[1,14 m$ e $2,36 m ]$

Signori ho cercato di risolvere il problema sfruttando l'ultima equazione consigliata, ovvero |d1-d2|=λ

Ho calcolato la lunghezza d'onda sfruttando la velocità del suono e la frequenza, poi ho sostituito a d1 e d2 i loro corrispondenti valori sfruttare il teorema di Pitagora. Il punto è che così l'equazione include radicali che rendono il tutto parecchio complesso, qualcuno può aiutarmi?

Autore

Risposta

MrRob

(@mrrob)

4 punti

livello:

Livello 0

3 Risposte
2 0 1

06/11/2022 00:30

mg · Accepted Answer

Hai fatto bene;

|d1-d2|=λ ;

λ = 340 / 700 = 0,486 m;

| radice(4^2 + x^2) - radice[4^2 + (3,50 - x)^2] |= 0,486;

si separano le radici; si elevano al quadrato entrambi i membri

radice[4^2 + (3,50 - x)^2] = radice(4^2 + x^2) - 0,486;

4^2 + (3,50 -x)^2 = 4^2 + x^2 + 0,486^2 - 2 * 0,486 * radice(4^2 + x^2);

Ci resta una radice sola al secondo membro.

16 + 3,50^2 + x^2 - 7,0 x = 16 + x^2 + 0,236 - 0,972 * radice(4^2 + x^2);

12,25 - 7,0 x - 0,236 = - 0,972 * radice(4^2 + x^2);

12,014 - 7,0 x = - 0,972 * radice(4^2 + x^2);

eleviamo al quadrato di nuovo per eliminare la radice:

(12,014 - 7,0 x)^2 = [- 0,972 * radice(4^2 + x^2)]^2;

144,34 + 49x^2 - 168,2 x = 0,945 * (4^2 + x^2);

49 x^2 - 168,2 x = - 144,34 + 0,945 * (16 + x^2);

49 x^2 - 168,2 x = - 144,34 + 15,12 + 0,945 x^2;

49x^2 - 0,945x^2 - 168,2 x = - 129,22;

48,1 x^2 - 168,2 x + 129,22 = 0;

avremo due soluzioni:

facciamo la ridotta - b/2 = + 168,2 / 2 = 84,1;

x = [+ 84,1+- radice(7072,8 - 48,1 * 129,22)] / 48,1;

x = [+ 84,1+- radice(857,32)] /48,1;

x = [+ 84,1 +- 29,3] / 48,1;

x1 = (84,1 + 29,3) / 48,1 = 2,36 m;

x2 = (84,1 - 29,3) / 48,1 = 1,14 m.

Ciao. @mrrob

mg

(@mg)

63562 punti

livello:

Genius I

9149 Risposte
5 5604 1235

16/11/2022 15:40

[Risolto] Problema di fisica (ambito suono)

Domande