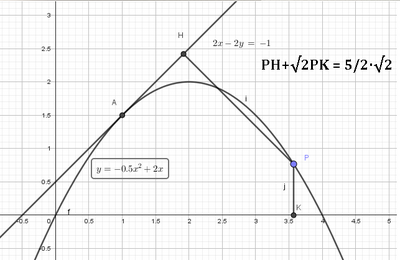
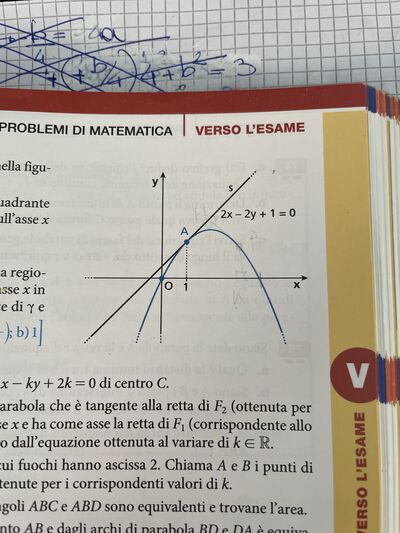
LEGGI IL GRAFICO Scrivi l'equazione della parabola $\gamma$ nella figura, che è tangente in $A$ alla retta $s$.
a. Determina sull'arco di $\gamma$ che appartiene al primo quadrante un punto $P$ e le sue proiezioni $H$ e $K$ sulla retta s e sull'asse $x$ in modo che: $\overline{P H}+\sqrt{2} \overline{P K}=\frac{5}{2} \sqrt{2}$.
b. Determina per quale valore di $c$ la retta $y=c$ divide la regione di piano del primo quadrante compresa tra $\gamma$ e l'asse $x$ in due parti, $A_1$ e $A_2$, in modo che $A_1$ contenga il vertice di $\gamma$ e $\frac{A_1}{A_2}=\frac{1}{2 \sqrt{2}-1}$.