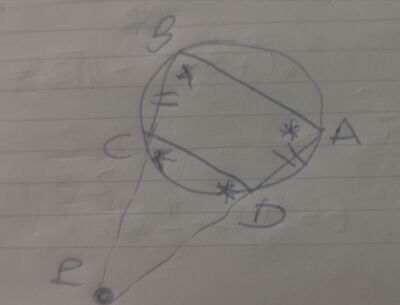
Siano A e B i punti d'intersezione di due circonferenze, non congruenti e parallele (A, B, C e D si susseguono sulla circonferenza in questo ordine). Sia P il punto d'intersezione dei prolungamenti delle corde BC e AD. Dimostra che i triangoli APB e CPD sono isosceli.
37
punti
Livello 0
Le corde AB e CD (parallele ma non congruenti) sono le basi del trapezio isoscele ABCD inscritto nella circonferenza. Gli angoli in A e B sono congruenti. Quindi il triangolo APB è isoscele sulla base AB.
Risultano congruenti anche gli angoli PCD e PDC in quanto corrispondenti di B ed A. Il triangolo CPD è isoscele sulla base CD
75876
punti
Genius II
Le circonferenze parallele mi mancano proprio ...grazie di aver colmata questa mia (assieme a tante altre) lacuna
103522
punti
Genius II
