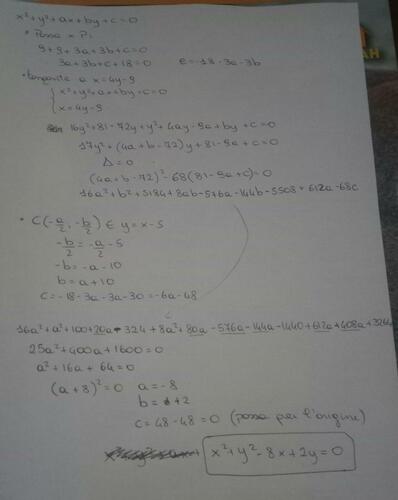[Risolto] Esercizio sulle coniche

Qui ci sono gli svolgimenti per trovare l'equazione della parabola e quella della circonferenza, ti resta da metterle a sistema e trovare il loro punto di intersezione e infine l'area del triangolo OPQ 

CHE SINTASSI CONTORTA, e che ortografia orribile!
------------------------------
Tre punti formano triangolo se non sono allineati.
L'area S del triangolo che ha i vertici
* O ≡ P1(x1, y1), P ≡ P2(x2, y2), Q ≡ P3(x3, y3)
è metà del valore assoluto di una semplice espressione delle coordinate (v. http://it.wikipedia.org/wiki/Triangolo#Formule_analitiche )
* S(OPQ) = (1/2)*|x1*(y2 - y3) - x2*(y1 - y3) + x3*(y1 - y2)|
Se tre punti sono allineati l'area del triangolo che li ha per vertici è zero.
------------------------------
La retta
* r ≡ x - 4*y + 9 = 0 ≡ y = (x + 9)/4
ha pendenza m = 1/4, e il punto P(3, 3) giace su di essa.
Le sue perpendicolari, con pendenza antinversa m' = - 1/m = - 4, formano il fascio
* p(q) ≡ y = q - 4*x
e quella per P è
* p(15) ≡ y = 15 - 4*x
------------------------------
Il centro C della circonferenza richiesta dev'essere sia sulla retta y = x - 5 [cioè essere C(k, k - 5)] che sulla p(15) [cioè essere C(k, 15 - 4*k)], da cui
* k - 5 = 15 - 4*k ≡ k = 4 → C(4, - 1)
Il raggio è la distanza
* |CP| = √17
da cui la circonferenza
* Γc ≡ (x - 4)^2 + (y + 1)^2 = 17
che passa per l'origine in quanto
* (0 - 4)^2 + (0 + 1)^2 = 17
------------------------------
Ogni parabola con
* asse y = 1
* apertura a != 0
* vertice V(w, 1)
ha equazione
* Γp ≡ x = a*(y - 1)^2 + w
Quella richiesta (tangente in P a r) deve anzitutto passare per P
* 3 = a*(3 - 1)^2 + w ≡ w = 3 - 4*a
da cui
* Γp ≡ x = a*(y - 1)^2 + 3 - 4*a
e poi avere uno e un solo punto comune con r.
Sistema: r & Γp ≡ (y = (x + 9)/4) & (x = a*(y - 1)^2 + 3 - 4*a)
Risolvente: a*((x + 9)/4 - 1)^2 + 3 - 4*a - x = 0
Discriminante: Δ(a) = (a - 1)^2
quindi
* Δ(a) = 0 ≡ a = 1
da cui infine
* Γp ≡ x = (y - 1)^2 - 1
che passa per l'origine in quanto
* 0 = (0 - 1)^2 - 1
------------------------------
I punti comuni alle due curve si ricavano da
* Γc & Γp ≡ ((x - 4)^2 + (y + 1)^2 = 17) & (x = (y - 1)^2 - 1) ≡
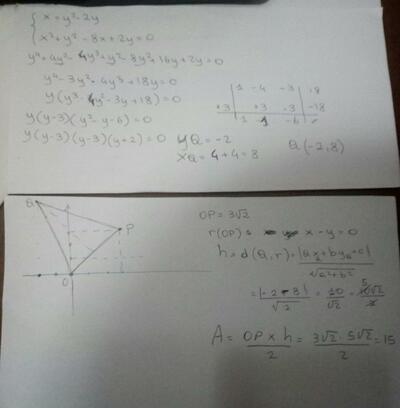
≡ O(0, 0) oppure P(3, 3) oppure Q(8, - 2)
da cui
* S(OPQ) = 15