Ho provato a svolgere questo esercizio ma non saprei nemmeno da dove iniziare, se qualcuno mi può dare una mano ne sarei molto grato!
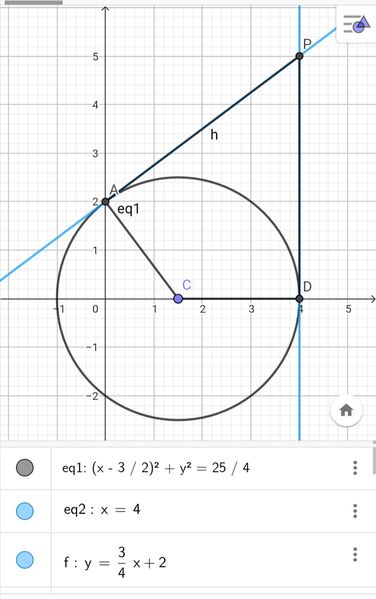
Scrivi l’equazione della circonferenza che ha il centro C sull’asse x e passa per i punti A(0; 2) e B(-1/2 ; - 3/2). Calcola l’ascissa del punto D di intersezione della circonferenza con il semiasse positivo delle ascisse e, dopo aver trovato le equazioni delle rette tangenti alla circonferenza in A e D, determina le coordinate del loro punto di intersezione P e l’area del quadrilatero APDC.
Risultati: x^2 +y^2-3x-4=0; D(4;0); x=4; y=3/4x+2;
P(4;5); 25/2.