[Risolto] Esercizio sul triangolo

Abbiamo un rettangolo con l'area Ar di 100 cm^2 e l'altezza hr di 4 cm.

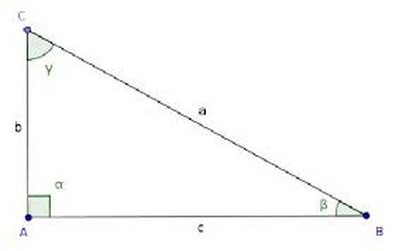
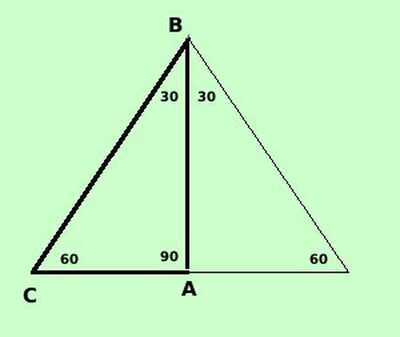
Abbiamo, inoltre, un triangolo rettangolo con gli angoli di 90, 60 e 30 gradi.

Le basi delle due figure hanno la stessa misura.

Calcola l'area e il perimetro del predetto triangolo.

rettangolo 

br = Ar/h = 100/4 = 25 cm 

 

triangolo 1 (cateto maggiore come base)

AB = br = 25 = 75/3

AC = 25√3/3 

BC = 2AC = 50√3 /3 

perimetro 2p = 25(3+√3+2√3)/3 = 75(1+√3)/3 = 25(1+√3)

area At = c*b/2 = 25*25√3 /6 = 625√3 /6 

 

triangolo 2 (cateto minore come base)

AC = br = 25 

AB = 25√3 

BC = 2AC = 50

perimetro 2p = 25(3+√3) 

area At = c*b/2 = 25*25√3 /2 = 625√3 /2 

 

triangolo 3 (ipotenusa come base)

c = br = 25 

a = 25√3/ 2 

b = c/2 = 25/2 

perimetro 2p = 25(1+√3 /2+1/2) = 25/2(3+√3) 

area At = a*b/2 = 625√3 /8  

 

Come base del triangolo rettangolo consideriamo l'ipotenusa.

Avendo gli angoli 30°, 60° e 90° è la metà di un triangolo equilatero, del quale  l'ipotenusa è il lato, il cateto minore sarà 12,5 cm ( metà lato) e l'altro cateto l'altezza del triangolo equilatero, ossia 12,5 * $\sqrt {3}$ = 21,65 cm

 

 

 

Base rettangolo = 25 cm;

Il triangolo rettangolo avrà per base 25 cm. Quale lato vuoi considerare come base? Un cateto o l'ipotenusa? Nel triangolo 30° 60° 90° L'ipotenusa è il doppio del cateto di fronte a  30°. Se l'ipotenusa è 25 cm, il cateto AC è 12,5 cm.

L'altezza h = radice(25^2 - (25/2)^2 ) = 25 * radice(3) /2 = 12,5 * radice(3).

Se la base del triangolo è il cateto AC = 25  cm, allora l'ipotenusa misura il doppio, cioè 50 cm.

 

io provo ad inserire le formule, ma non riesco mai, comunque volevo scrivere "radice di 3"

A mio modesto parere la frase iniziale della risposta di Carmy ("Come base del triangolo rettangolo consideriamo l'ipotenusa.") in una qualsiasi sede d'esame (dalla licenza elementare alla laurea in economia) le avrebbe fruttato un voto insufficiente con la motivazione "semplificazione gratuita".
Chi propone un problema e poi ne corregge gli elaborati consegnati di solito non gradisce che i candidati si autosemplifichino il compito tagliandone via una parte.
Quando la traccia di un tema d'esame è VOLUTAMENTE indeterminata (fra gli obiettivi delle materie tecniche c'è di solito la capacità di organizzare al meglio i materiali a disposizione) la consegna ha la forma "Poste le ipotesi aggiuntive che ritengono opportune, i candidati facciano questo, quest'altro e quest'altro ancora.".
SE MANCA LA CONSEGNA DI "porre ipotesi aggiuntive" IL FARLO COSTITUISCE DEMERITO: chi ha proposto il problema intende valutare come i candidati affrontino complessità e incertezze.
Quindi (ancora a mio modesto parere) dire "Poi, però, mi sono bloccato." è più corretto che porre ipotesi non richieste: l'equivoco si affronta esplorando le alternative e non adottandone una a casaccio.
Bloccarsi a questo serve, a riflettere con calma sui significati del testo.
Poi però si dovrebbe proseguire!
------------------------------
Il vero significato del problema (quello che risulta dal bloccarsi per riflettere) è
«Calcolare area e perimetro di un triangolo rettangolo che è metà di un triangolo equilatero in funzione della lunghezza di uno dei suoi lati, PER TUTT'E TRE I LATI.»
Tutto ciò che occorre rammentare per risolvere il problema è che
* il cateto minore "a = c/2" è metà dell'ipotenusa "c = 2*a", lato dell'equilatero;
* il cateto maggiore "b = (√3/2)*c" è l'altezza dell'equilatero;
* l'altezza relativa all'ipotenusa è "h = a*b/c".
Sapendo esprimere due dei lati in funzione del terzo si possono calcolare
* area A = a*b/2 = c*h/2
* perimetro p = a + b + c
nei tre casi.
---------------
Dato "a = 25"
* b = (√3)*a
* c = 2*a
* A = a*b/2 = (√3/2)*a^2
* p = a + b + c = (3 + √3)*a
---------------
Dato "b = 25"
* a = b/√3
* c = 2*b/√3
* A = a*b/2 = b^2/√3
* p = a + b + c = (1 + √3)*b
---------------
Dato "c = 25"
* a = c/2
* b = (√3/2)*c
* A = a*b/2 = (√3/4)*c^2
* p = a + b + c = (3 + √3)*c/2