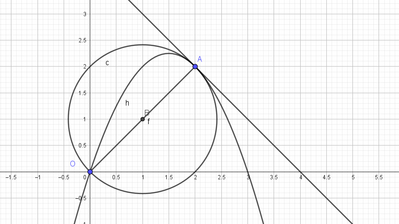
In un sistema di assi cartesiani sono dati i punti $O(0,0)$ e $A(2,2)$, e la circonferenza avente per diametro il segmento $O A$. Determina l'equazione della parabola, con l'asse parallelo all'asse delle ordinate, passante per i due punti dati e tale che abbia in A come tangente la retta tangente alla circonferenza.
Qualcuno potrebbe darmi una mano con l'esercizio?
Grazie in anticipo!
134
punti
Livello 1
y = a·x^2 + b·x dovendo passare per l'origine O (quindi c=0)
2 = a·2^2 + b·2 passa per A ---> 4·a + 2·b = 2
Retta tangente alla circonferenza in A deve avere m = -1 (diametro e retta sono fra loro perpendicolari)
y - 2 = - 1·(x - 2)----> y = 4 - x
Essendo b = 1 - 2·a, la parabola si scrive:
y = a·x^2 + (1 - 2·a)·x
Applico le formule di sdoppiamento in A:
(y + 2)/2 = a·(x·2) + (1 - 2·a)·(x + 2)/2
ottengo: y = x·(2·a + 1) - 4·a
Confronto le due equazioni in grassetto . Devono essere verificate le due equazioni:
{2·a + 1 = -1
{- 4·a = 4
Quindi: a = -1
b = 1 - 2·(-1)-----> b = 3
Parabola: y = (-1)·x^2 + 3·x----> y = 3·x - x^2
96624
punti
Genius II
@lucianop Grazie per il grafico!
Hai pure la risoluzione analitica.
@lucianop Grazie mille, non avevo considerato che il diametro fosse perpendicolare... Grazie mille 🙂
Di nulla. Buona serata.
