Di due luoghi $\gamma_1$ e $\gamma_2$ sono date le equazioni parametriche:
$$
\gamma_1:\left\{\begin{array}{l}
x=\frac{h}{\sqrt{1+h^2}} \\
y=\frac{1}{\sqrt{1+h^2}}
\end{array} \quad \gamma_2:\left\{\begin{array}{l}
x=2-k \\
y=-k^2+4 k-3
\end{array} \quad \operatorname{con} h \in R \wedge k \in R \right.\right.
$$
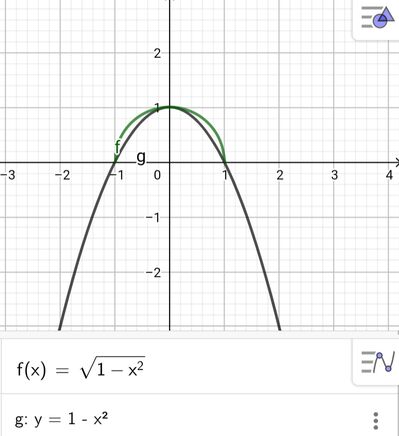
a. Scrivi le equazioni cartesiane dei due luoghi. $\quad\left[\gamma_1: y=\sqrt{1-x^2} ; \gamma_2: y=1-x^2\right.$ -
b. Dopo avere rappresentato graficamente i due luoghi, giustifica che essi delimitano, nel primo e nel secondo quadrante, due parti di piano di uguale area e determina tale area.