[Risolto] equilibrio

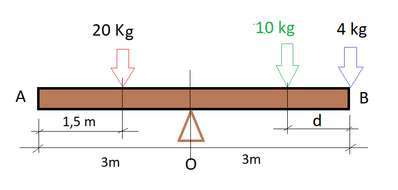
Un'asta omogenea di estremità A e B ha una lunghezza di 6,0 m e un peso di 150 N. Essa è sistemata su un supporto posizionato esattamente al centro O. Un oggetto puntiforme dalla massa di 20 kg è adagiato a una distanza di 1,5 m da A e uno dalla massa di 4,0 kg è posizionato su B. A che distanza d da B si deve posizionare un oggetto dalla massa 10 kg affinché l'asta si trovi in equilibrio?

La sommatoria dei momenti orari ed antiorari rispetto ad O deve essere zero ; poiché il supporto è equidistante da A e B il suo contributo all'equilibrio è nullo e non rimane che equilibrare i momenti generati dalle masse 

momento antiorario 

g(20*(3-1,5) = 30*g N*m

momento orario 

g(4*3+10(3-d) = g(12+30-10d) N*m

g si semplifica

30 = 42-10d

d = (42-30)/10 = 1,20 m 

Indichiamo con x il braccio della forza di modulo 10g, scegliendo come polo il punto medio dell'asta. 

Nulli sono quindi i momenti generati dalla forza peso dell'asta e dalla reazione vincolare del supporto (i bracci sono nulli) 

20g*1,5=4g*3 + 10g*x

x=1,8 m (dal centro) 

Quindi la distanza da B è 1,2 m