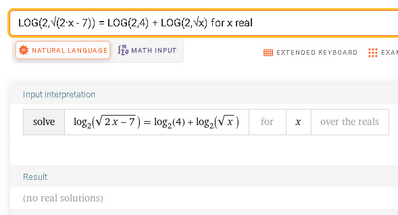
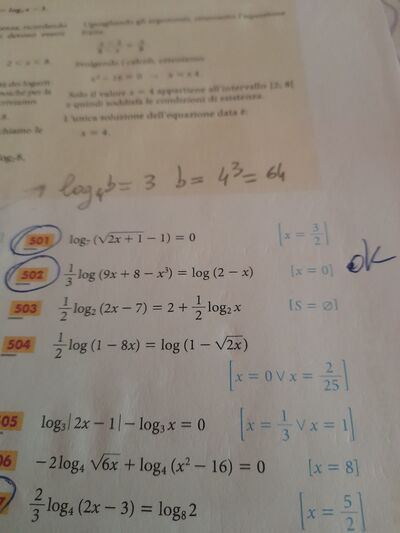Buongiorno a tutti; allego alla presente 2 files : il primo contiene l'esercizio n. 503 che ha come risultato insieme vuoto, equazione impossibile e il secondo il mio svolgimento, che, non dando la stessa soluzione deve per forza contenere uno o più errori. Chiedo gentilmente se qualcuno vuole darmi un aiuto e anche, se possibile, farmi notare dove sbaglio, perché, a mio avviso, é altrettanto utile per non ripetere nuovamente l'inesattezza nel futuro. Grazie a tutti nuovamente per il vostro costante supporto e per la vostra pazienza.