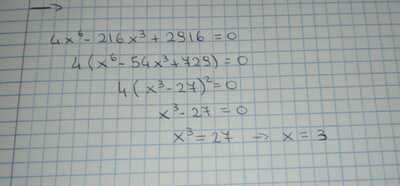Ciao!
Ho questa equazione:
(x^4+3x^5-3x^2-11x-6)(4x^6-216x^3+2916)=0
Il primo fattore lo scompongo in (x+1)^2(x-2)(x+3)
Il secondo 4(x-3)^2(x^2+3x+9)^2
Quindi ottengo:
4(x-3)^2(x^2+3x+9)^2 (x+1)^2(x-2)(x+3)=0
La traccia dell'esercizio consiste nel risolvere l'equazione mediante legge di annullamento del prodotto.
Se non fosse per (x^2+3x+9)^2 sarebbe abbastanza semplice, ma siccome non ho ancora trattato le equazioni di secondo grado, come riconduco questa al primo grado dal momento che non mi sembra fattorizzabile?