Ciao! In questa equazione:
|x-1|=2/(|x+1|)-1
Impostando i tre sistemi:
x<-1 -1<x<1 x>=1
1-x=2/(-x-1)-1 x-1=2/(-x-1)-1 x-1=2/(x+1)-1
Trovo come soluzioni:
x=(1-√17)/2 x=1
Stando ai calcolatori, una soluzione è anche x=0, ma non riesco a trovarla, come mai?
105
punti
Livello 1
Ciao. I tre moduli si liberano:
{ABS(x - 1) = x - 1
{se x ≥ 1
---------------------------
{ABS(x - 1) = 1 - x
{se x < 1
--------------------------
{ABS(x + 1) = x + 1
{ se x ≥ -1
-------------------------
{ABS(x + 1) = - (x + 1)
{se x < -1
-------------------------
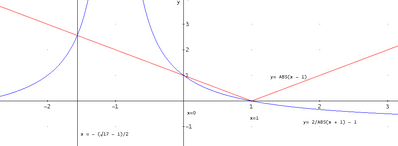
Tenendo conto di queste condizioni, l'equazione: ABS(x - 1) = 2/ABS(x + 1) - 1
si riporta alla soluzione di 3 sistemi di cui poi, dovrai considerare l' unione delle 3 soluzioni:
{1 - x = 2/(- (x + 1)) - 1
{x < -1
---------------------------
{1 - x = 2/(x + 1) - 1
{-1 <x < 1
---------------------------
{x - 1 = 2/(x + 1) - 1
{x ≥ 1
-----------------------------
La soluzione del primo sistema è:
x = - (√17 - 1)/2 (quindi: x = -1.561552812) accettabile!
La soluzione del secondo sistema è:
x = 0 accettabile
La soluzione del terzo sistema è:
[x = 1] accettabile
DEVI STARE ATTENTO ANCHE AGLI UGUALI (esatti come li ho scritti io!) . Controlla i sistemi e stai più attento.
83235
punti
Genius II
Nel sistema
{1 - x = 2/(x + 1) - 1
{-1 ≤ x < 1
Anch'io avevo scritto -1 ≤ x < 1 ma poi ho scritto -1 < x < 1 poichè per x=-1 l'equazione corrispondente perde significato, giusto?
Ho corretto, grazie.
Se -1 < x < 1
1 - x = 2/(x+1) - 1
ed essendo x + 1 > 0
1 - x^2 = 2 - (x + 1)
1 - x^2 = 2 - x - 1
x - x^2 = 0
x(1 - x) = 0
x = 0 V x = 1
41854
punti
Livello 7
Grazie, avevo fatto confusione nello studiare i segni degli argomenti
