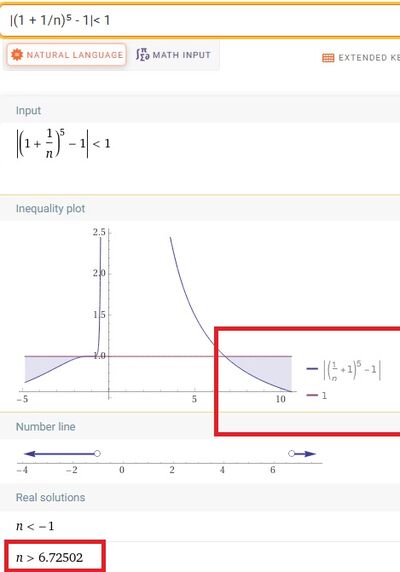
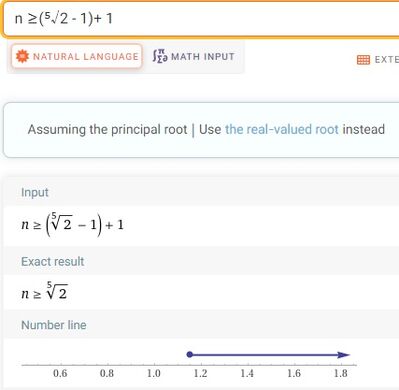
Salve, in alcuni appunti è riportato (si parla della definizione di limite per la successione in questione) che la disequazione in valore assoluto |(1 + 1/n)⁵ - 1| < 1 implica che n ≥ [⁵√2 - 1] + 1, dove le quadre indicano la parte intera. Il modo in cui l'ho risolta è (prendendo solo la disequazione di destra):
(1 + 1/n)⁵ < 2
1/n < ⁵√2 - 1
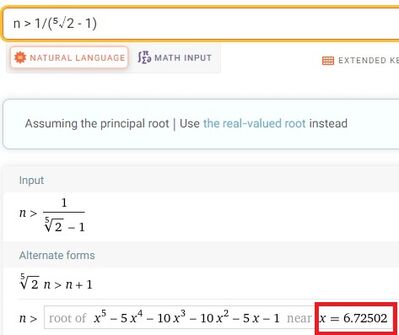
n > 1/(⁵√2 - 1)
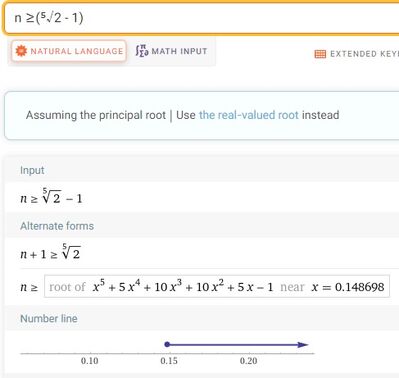
Da qui, dato che voglio n > un naturale, prendo la parte intera del secondo membro + 1. Tuttavia, nella soluzione originale, si dovrebbe avere ⁵√2 - 1 e non il suo reciproco. Sto commettendo un errore nel risolvere o è la soluzione ad essere effettivamente sbagliata? Grazie in anticipo.