Ciao a tutti, ho cominciato a studiare le disequazioni ed ancora devo conoscere le varie sfumature che quest'ultime celano. 😀
Ho questa equazione: $\frac{1}{x-2}-\frac{2}{x-3\:}\le \frac{x-5}{x^2-5x+6}$ , CE: $x\ne 2\:\wedge \:x\ne 3$
Svolgendo i calcoli si arriva a: $\frac{-2x+6}{\left(x-2\right)\left(x-3\right)}\le 0$.
Prima idea:
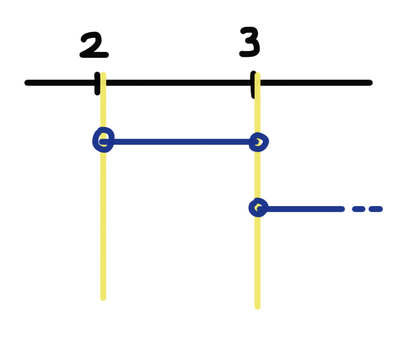
Calcolo il segno di questa disequazione e come soluzione ottengo $2<x<3\:\vee \:x>3$
Seconda idea:
Continuo con i calcoli, raccolgo $-2$ dunque $\frac{-2\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\le 0\:$ e poi semplifico: $\frac{-2}{\left(x-2\right)}\le 0\:$.
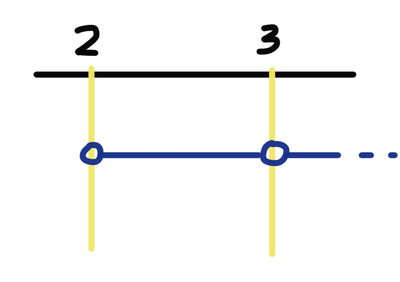
Moltiplico e divido tutto per $-1$ e $2$ e giungo a: $\frac{1}{x-2}\ge 0$ la cui soluzione è $x>2\:\wedge \:x\ne 3$.
Ora, quello che mi chiedo, le due soluzioni sono equivalenti?
Scrivere $2<x<3\:\vee \:x>3$ è la stessa cosa di $x>2\:\wedge \:x\ne 3$ ?
Ad esempio, se avessi solo la prima, potrei ricavare la seconda? E viceversa?
Tutto si basa sul saper interpretare le scritture? (...sembra una cosa biblica 😆!)
Perdonate l'ignoranza ma non ho ancora molta familiarità con le disequazioni e non vorrei compiere errori, se avete qualche trick da pro da consigliarmi son tutto orecchie hehe 🧐