BRAVO WALTER, CONGRATULAZIONI!
Un nuovo iscritto che s'è letto il Regolamento prima di scrivere la domanda è un'assoluta novità.
Che bello avere un testo su cui fare Copia/Incolla nel mio editor!
Però, ehm ... beh, la figura ci sarebbe proprio voluta: vado a vedere l'invio successivo al link
https://www.sosmatematica.it/forum/postid/17729/
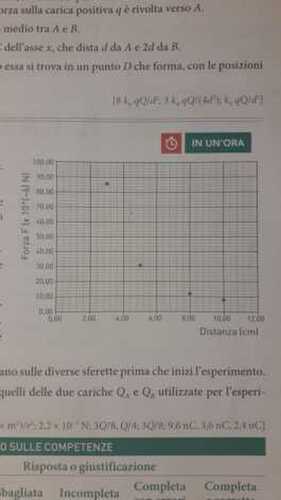
e lì trovo la foto di una figura, ma è buia e sfocata; le ascisse le intuisco e le ordinate le devo indovinare, inoltre i punti sfocati sembrano giganteschi.
==============================
Sfere conduttrici identiche vuol dire di identica capacità; su supporto isolante, vuol dire che ciascun contatto equiripartisce la carica totale senza dispersioni.
Le cariche di (A, B, C) evolvono secondo lo schema
(q, 0, 0)
(q/2, q/2, 0)
(q/2, q/4, q/4)
((3/8)*q, q/4, (3/8)*q)
------------------------------
La forza di Coulomb fra le due cariche puntiformi (il prefisso "x" sta per "illeggibile")
* qA = (3/8)*q xC
* qB = q/4 xC
poste in aria a distanza di d cm è
* F = (1/(4*π*ε))*((3/8)*q)*(q/4)/(d/100)^2 xN
dove la permittività dell'aria è
* ε = εr*ε0 = (8.85418781762/10^12)*(1.00059) = 8.8594117884323958/10^12 F/m
quindi invece della solita approssimazione "k = 1/(4*π*ε0) ~= 8.85/10^12" si deve usare "8.86/10^12 = 886/10^14" o meglio l'intero valore di 17 cifre salvo poi approssimare il risultato finale.
NON IN QUESTO CASO, PERO': prendendo ad occhio distanze e forze basta e avanza l'approssimazione a tre cifre significative, da cui
* F = (1329/(16*10^10))*q^2/d^2 ~= (8.31/10^9)*q^2/d^2
------------------------------
Dalla figura rilevo (intuendo e indovinando, quindi a numeri interi) le seguenti coppie (cm, xN)
* (3, 86), (5, 32), (8, 12), (10, 8)
da cui
* ((8.31/10^9)*q^2/3^2 = 86), ((8.31/10^9)*q^2/5^2 = 32), ((8.31/10^9)*q^2/8^2 = 12), ((8.31/10^9)*q^2/10^2 = 8) ≡
≡ (q ~= 305190), (q ~= 310273), (q ~= 304005), (q ~= 310273)
---------------
Suggerirei di usare le stime
* q ~= 306000 xC
* q^2 ~= 9.3636*10^10 xC^2
* (8.31/10^9)*q^2 ~= 778 xN^2
nel fare i calcoli per rispondere alle domande.
==============================
RISPOSTE AI QUESITI
------------------------------
A) "Individua la legge sperimentale che si può dedurre dall'analisi dei dati."
* F(d) = 778/d^2
quindi dal confronto di
* (3, 86), (5, 32), (6, x), (8, 12), (10, 8)
con
* (3, 778/9), (5, 778/25), (6, 389/18), (8, 389/32), (10, 389/50) ~=
~= (3, 86.44), (5, 31.12), (6, 21.61), (8, 12.16), (10, 7.78)
si trova, sui quattro dati, la devianza
* D = (86 - 778/9)^2 + (32 - 778/25)^2 + (12 - 389/32)^2 + (8 - 389/50)^2 =
= 54159577/51840000 ~= 1.045
da cui
* σ = √(D/(n - 1)) ~= √((54159577/51840000)/3) ~= 0.59 xN
------------------------------
B) "... la orza che si sarebbe dovuta misurare ..."
* F(6) = 778/6^2 ± σ ~= 21.61 ± 0.59 xN
------------------------------
C + D) "Individua quanto valgono ... le tre cariche ..."
* q ~= 306000 xC
* qA = (3/8)*q ~= (3/8)*306000 = 114750 xC
* qB = q/4 ~= 306000/4 = 76500 xC