Gli abitanti di due villaggi attingono acqua da due pozzi situati ad una certa distanza da entrambi i villaggi. A causa di ricorrenti siccità, un antico accordo stabilisce che ognuno dei villaggi possa utilizzare i due pozzi a disposizione, e quindi da ogni villaggio partono due o più sentieri che arrivano a ciascuno dei pozzi ( passando anche da villaggio a villaggio ). La situazione è dunque schematizzata dal seguente schema :
$villaggio$ $villaggio$
$pozzo$ $pozzo$
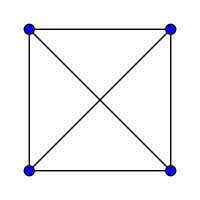
Col tempo si è però sviluppata una rivalità tra le due comunità, per cui possono verificarsi incidenti qualora abitanti di diversi villaggi si incontrino negli incroci tra i sentieri. Alcuni abitanti di un villaggio proposero di risolvere il problema tracciando nuovi sentieri per far si che i nuovi cammini non potevano in alcun modo essere intercettati. Dunque, la questione è capire se il nostro schema possa essere disegnato su un piano in modo che i sei lati non si intersechino in alcun punto ( ad eccezione, ovviamente, dei vertici ). La risposta è si e lo schema risulta essere :
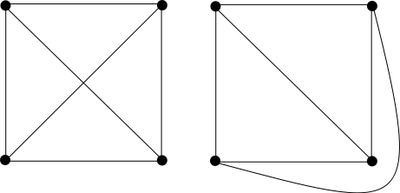
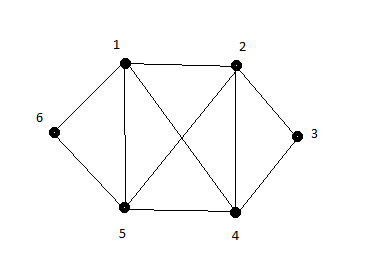
Quali dei seguenti schemi può essere disegnato in modo che i lati non si intersechino?
Il quesito in questione, per chi non lo sapesse, parla della $teoria$ $dei$ $grafi$. Questa disciplina si occupa dello studio di oggetti discreti molto particolari chiamati appunto $grafi$. Questi oggetti possono rappresentare una varietà di situazioni della realtà e molto spesso consentono di semplificare lo studio di algoritmi informatici.
Tornando a noi; per riuscire a trovare una soluzione al quesito, dobbiamo innanzitutto capire cosa sono i $grafi$ $planari$ ( oggetti fondamentali per la risoluzione dell'esercizio ). Introduciamo la cosa in maniera poco formale :
Si chiama $grafo$ $planare$ un grafo che può essere tracciato sul piano, in modo tale che i suoi lati non si incrocino mai, eccetto che in un vertice al quale siano entrambi incidenti. Nell'esempio fatto sopra possiamo notare che sebbene il grafo $completo$ $K_{4}$, ( con questo termine indichiamo un grafo in cui i vertici sono a due a due adiacenti, quindi collegati da almeno un lato ) venga di solito rappresentato con i lati intersecati, esso può essere rappresentato con lati non intersecati. In conclusione $K_{4}$ è un grafo planare.
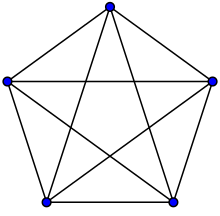
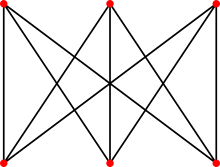
Possiamo anche trovare esempi di grafi non planari come il grafo completo $K_{ 5 }$ e il grafo $K_{ 3, 3 }$ ( il cui nome ufficiale è $grafo$ $bipartito$ di tipo ( $3$, $3$ ) ). Dunque sarebbero il primo e l'ultimo grafo proposti per la risoluzione del quesito. Per verificare se i due grafi erano o meno planari, bastava manipolare i vari lati e vedere se era possibile rappresentare sul piano dei nuovi grafi senza che i lati si intersechino. In conclusione i grafi risultano essere non planari.
Una questione di fondamentale importanza è che aggiungendo lati e vertici a questi due grafi, quindi ingrandendo in modo considerevole il diagramma, il risultato sarà sempre lo stesso. Quindi ogni grafo avente come base un grafo non planare sarà sicuramente non planare.
Da queste considerazioni possiamo osservare, a questo punto, che quando un grafo risulta avere un sottografo isomorfo ( quindi avente le stesse proprietà ) a $K_{5}$ o a $K_{3, 3}$ di conseguenza non è planare.
Presupponiamo che la ricerca dei grafi planari è stata, per molti anni, uno dei maggiori studi da parte di molti matematici, infatti essi tentarono in tutti i modi di sintetizzarli per poterli identificare ( cosa che però non vi riuscì ). Ma finalmente, nel $1903$, il problema fu risolto dal matematico polacco $k.$ $Kuratowski$, che dimostrò il seguente teorema :
$Un$ $grafo$ $è$ $planare$ $se$ $e$ $solo$ $se$ $non$ $contiene$ $alcun$ $sottografo$ $isomorfo$ $a$ $K_{5}$ $o$ $K_{ 3, 3 }$.
Attraverso queste premesse ormai risulterà essere chiaro quando un grafo è planare quindi cerchiamo di dare una risposta soddisfacente al nostro quesito. Come già sappiamo il primo e l'ultimo grafo non sono planari poiché isomorfi a $K_{5}$ e $K_{ 3, 3 }$. Ma il secondo risulta esserlo. Possiamo accorgercene manipolando i vari lati fino a rappresentarlo in una forma che rispetti la definizione oppure notare che non possiede sottografi isomorfi a $K_{5}$ o $K_{ 3, 3 }$.