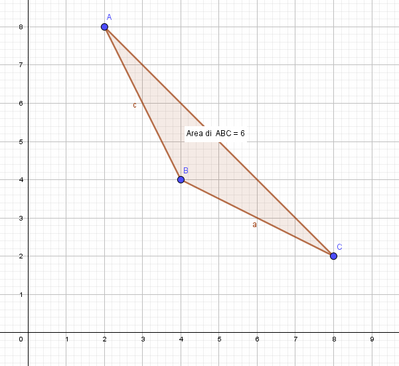
Calcola l'area della figura piana i cui vertici sono i punti di intersezione dell'equazione della circonferenza : x^2 + y^2 - 18x - 18 y + 112 = 0 e dell'iperbole equilatera, riferita ai propri asintoti, xy = 16.
Risposta : 6
P.S. Ho messo a sistema le 2 equazioni e mi risultano queste radici del sistema ; y1 = 2 ; y2= 4 ; y3= 8 e conseguentemente x1 = 8; x2= 4 ; x3= 2. Quindi i vertici hanno coordinate (8;2), (4;4), (2;8), ma unendoli non si forma nessuna figura piana... Qualcuno, come sempre, mi può dare un aiuto? Grazie anticipatamente a chi vorrà darmi una mano.