Trovare i possibili rettangoli col calcolo combinatorio

Come faresti operativamente a costruire il rettangolo ?

Scegli una colonna ( 5 punti ) e ne fissi due, l'ordine non conta ed hai C(5,2) modi

per farlo.

Se la colonna che hai scelto é la prima puoi sceglierne un'altra in 5 modi e i due

ulteriori vertici saranno determinati dal fatto che devono essere alla stessa altezza

dei due già scelti.

Se é la seconda hai 4 modi di sceglierne una a destra, se é la terza tre modi, se é

la quarta in due modi, se é la quinta un solo modo, se é la sesta nessuno.

Il numero cercato é quindi C(5,2) * [5 + 4 + 3 + 2 + 1 + 0] = 10*15 = 150.

Non so se sia questa la somma di Gauss, ma mi sembra plausibile.

Io farei il prodotto:

comb(5,2)*comb(6,2)=(5*4/2!)*(6*5/2!)=10*15=150

in quanto devi prendere 2 vertici su 5 come altezza del rettangolo e 2 vertici su 6 come base del rettangolo. L’ordine non conta.

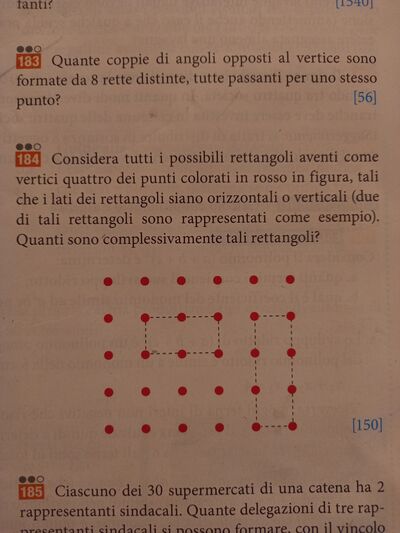
Per potere nel discorso riferirmi ai punti della griglia li nomino con una coppia di indici [riga, colonna] da [1, 1] per riferirmi a quello della riga #1 in colonna #1 (il primo in alto a sinistra), a [i, j] per quello della riga #i in colonna #j, a [m, n] per quello della riga #m in colonna #n (l'ultimo in basso a destra): per questa griglia [m, n] = [5, 6].
------------------------------
Come ESEMPIO DI CONTEGGIO inizio dalla Colonna #1
Vertice[1, 1]: per ogni vertice inferiore [r ∈ {2, 3, 4, 5}, 1] e ogni vertice destro [1, c ∈ {2, 3, 4, 5, 6}] ci sono 4*5 = 20 rettangoli.
Vertice[2, 1]: per ogni [r ∈ {3, 4, 5}, 1] e ogni [2, c ∈ {2, 3, 4, 5, 6}] ci sono 3*5 = 15 rettangoli.
E così via ordinatamente contando solo i rettangoli con vertici in basso e a destra del vertice pivot (quelli in alto e a sinistra sono già stati contati).
------------------------------
CONTEGGIO GENERICO
Come vertice in alto a sinistra si assuma [i, j]: per ogni [r ∈ {i + 1, ..., m}, j] e ogni [i, c ∈ {j + 1, ..., n}] ci sono (m - i)*(n - j) rettangoli.
I possibili valori di i vanno da 1 ad m - 1.
I possibili valori di j vanno da 1 ad n - 1.
Quindi su una griglia di m righe ed n colonne si possono tracciare un numero totale T di rettangoli dato da due somme annidate
* T = Σ [i = 1, m - 1] (Σ [j = 1, n - 1] (m - i)*(n - j))
dove, poiché il primo fattore del sommando non dipende da j, lo si può porre in evidenza fra tutti gli addendi e scrivere
* T = Σ [i = 1, m - 1] (m - i)*(Σ [j = 1, n - 1] (n - j))
e su questa forma si può ripetere egual considerazione sul secondo fattore, quindi
* T = (Σ [j = 1, n - 1] (n - j))*Σ [i = 1, m - 1] (m - i)
Dopo aver separato le due somme le si riconosce ciascuna come la nota somma di un certo numero d'interi consecutivi (somma di Gauss, a nove anni) e perciò
* Σ [i = 1, m - 1] (m - i) = (m - 1)*m/2
* Σ [j = 1, n - 1] (n - j) = (n - 1)*n/2
Così s'è ricavata, in funzione delle dimensioni della griglia, la formula che dà il numero totale di rettangoli possibili
* T(m, n) = ((m - 1)*m/2)*((n - 1)*n/2) = (m*n/4)*(m - 1)*(n - 1)
------------------------------
NEL CASO IN ESAME ([m, n] = [5, 6])
* T(5, 6) = (5*6/4)*(5 - 1)*(6 - 1) = (15/2)*4*5 = 150
che è proprio il risultato atteso.