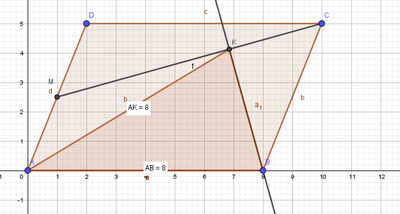
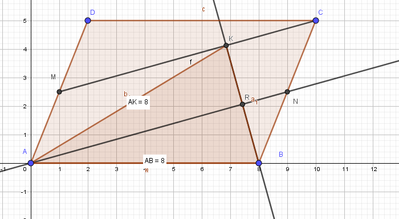
In un parallelogramma $A B C D$, sia $M$ il punto medio di $A D$. Indicata con $K$ la proiezione di $B$ sulla retta $K$ ic dimostra che il triangolo $A B K$ è isoscele sulla base $B K$, seguendo i passi qui indicati.
a. Traccia la retta passante per $A$ e parallela a $M C$ e indica con $R$ il suo punto d'intersezione con la retta $B K$.
b. Traccia la retta passante per $B$ e parallela a $M C$ e indica con $S$ il suo punto d'intersezione con la retta $A D$.
c. Dimostra che $A S \cong A M$.
d. Applica il piccolo teorema di Talete. Che cosa puoi dire dei segmenti $B R$ e $R K$ ?
e. Considera il triangolo $A K B$. Quale proprietà ha l'altezza relativa a $B K$ ? Perché?
f. Deduci che $A B \cong A K$.