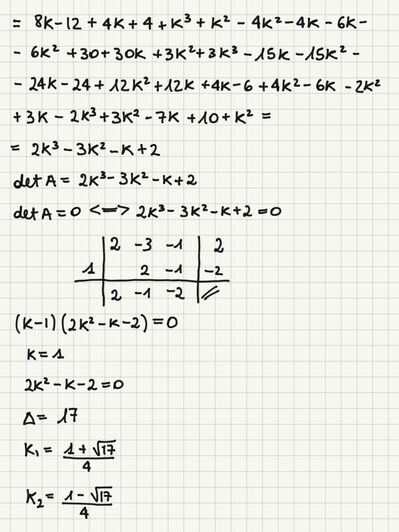Salve a tutti, sono nuova da queste parti!
avrei bisogno di un disperato aiuto nel risolvere questo tipo di sistemi lineari al variare del parametro k, se possibile qualcuno mi fa vedere l’esercizio svolto
Dopo aver definito la matrice completa, usato il metodo di eliminazione di gauss, e calcolato il determinante, quali sono i passaggi per questo tipo di statemi?
grazie mille a chi mi darà una mano nel farmi vedere l’esercizio svolto. 🤞🏻