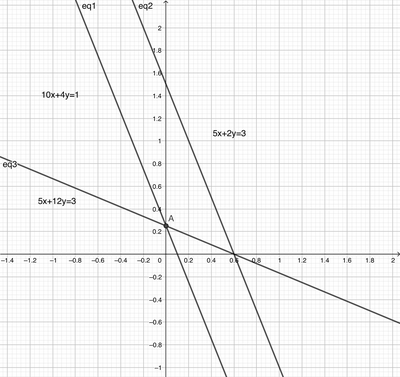
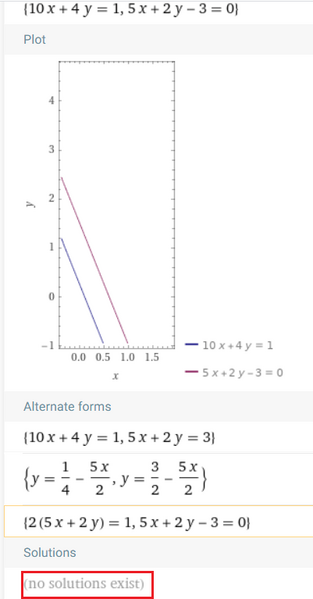
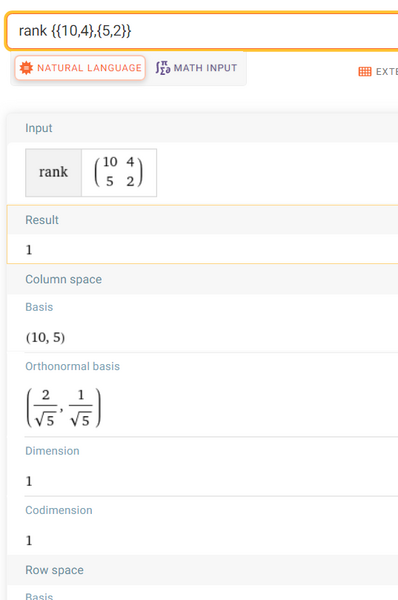
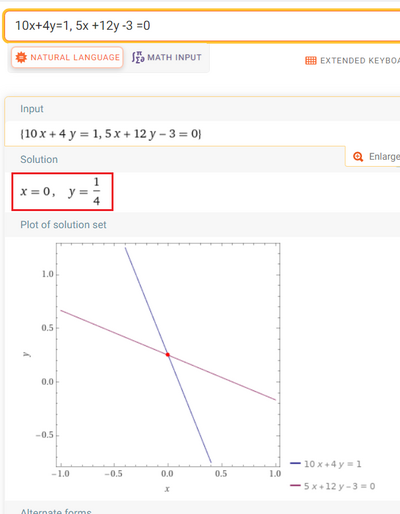
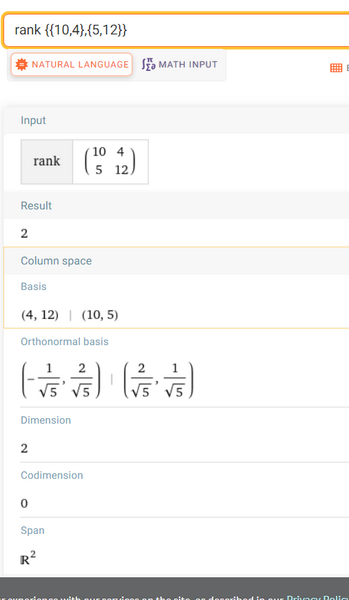
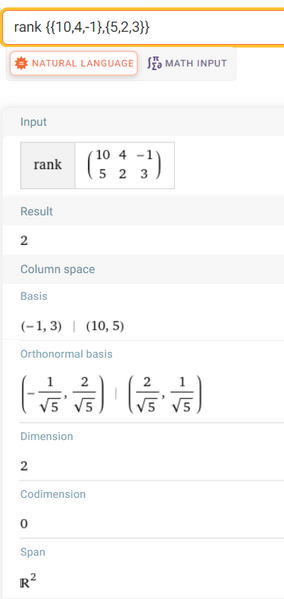
Detto $S$ l'insieme delle soluzioni dell'equazione $10 x+4 y=1$ e $S^{\prime}$ l'insieme delle soluzioni dell'equazione $5 x+k y-3=0$, con $k \in R$, determina per quale valore di $k$ risulta $S \cap S^{\prime}=\varnothing e$ per quale valore di $k$ risulta:
$$
S \cap S^{\prime}=\left\{\left(0 ; \frac{1}{4}\right)\right\}
$$
34
punti
Livello 0
Il problema chiede quindi per quali valori di k il sistema lineare in x ed y:
{10x+4y=1
{5x+Ky=3
è
1) impossibile
2) determinato e avente soluzione
{x=0
{y=1/4
1) E’impossibile se i coefficienti delle incognite sono in proporzione ma non lo sono i termini noti. Quindi deve essere k=2.
infatti: 10/5 = 4/2 =2
ed il rapporto fra i termini noti non fornisce 2 ma 1/3
2) Sostituiamo x=0 nelle due equazioni:
{4y=1 ————->y=1/4
{ky=3—————> k=3/y————->k =12
Quindi la risposta K=12
77305
punti
Genius II
In tal caso la spiegazione grafica è
1) le rette sono parallele e distinte
2) sono incidenti nel punto (0,1/4)
@lucianop grazie, gentilissimo
occorre e basta perchè S intersezione S' = vuoto che le due rette siano parallele e non coincidenti quindi che a b e a' b' siano in proporzione ... e che ciò non accada per i termini noti c e c'
10: 4 = 5: k ---> k =2 e c/c' = - 1/3 non valendo 2 non è in prop.
mentre perchè tale intersezione si riduca a P(0,1/4) basta e occorre che passino per P e non siano coincidenti ....
10*0 + 4*1/4 = 1 ---> ok
5*0 + k*1/4 -3 =0 ---> k = 12 ---> OK!
sulla non coincidenza delle rette
p.s.
su wolfram sono a sistema espressioni divise da una semplice "virgola"
5664
punti
Livello 5
@nik grazie mille
Le soluzioni del sistema delle rette
* (r ≡ 10*x + 4*y = 1 ≡ y = 1/4 - (5/2)*x) & (s(k) ≡ 5*x + k*y - 3 = 0 ≡ y = (3 - 5*x)/k)
sono
* (x = (k - 12)/(10*(k - 2))) & (y = 5/(2*(k - 2)))
che è un insieme vuoto per k = 2 (r ed s(k) avrebbero la stessa pendenza m = - 5/2, ma con diverse intercette).
---------------
Per ottenere
* (x, y) = (0, 1/4)
occorre che abbia soluzione il sistema delle coordinate
* ((k - 12)/(10*(k - 2)) = 0) & (5/(2*(k - 2)) = 1/4) ≡ k = 12
51569
punti
Genius I
@exprof ..great job
