problema traiettoria

Question

Salve, scusate nuovamente il disturbo, ma i problemi che riguardano moto parabolico e traiettoria sono ostici per me.

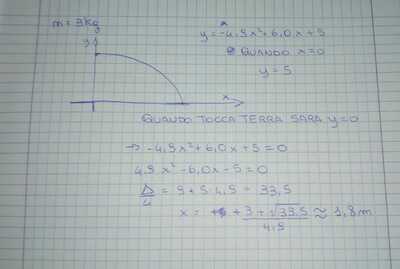
Un corpo di 3 kg viene lanciato da un punto che nel sistema di riferimento corrisponde a x=0. A che distanza dall'origine il corpo la cui traiettoria è data da y= -4.9x^2+6.0x+5.0 con x in m ed y in metri, tocca terra?

Moto parabolico

Lungo l'asse x è MRU

x(t)=v*t

Lungo l'asse y è MRUA

y(t)=y+v0t-1/2gt^2

Ritornando al metodo che mi avete gentilmente spiegato la scorsa volta, in un problema simile:

ricavo:

t=x(t)/v0x

sostituisco nella seconda equazione:

y(t)= y+v0y/v0x(x)-1/2g(x/v0)^2

y0=5.0

v0y/v0x=6.0

1/2g*1/(v0x^2)=-4.9

Ricavo v0x dall'ultima equazione è risulta 1.

Ricavo v0y dalla seconda e risulta 6.0.

Facendo la legge oraria:

x=5.0+6.0-4.9= 6.0m

Corretto, come procedimento? grazie

I

Autore

Risposta

Chiarachiaretta

(@chiarachiaretta)

824 punti

livello:

Livello 1

733 Risposte
233 0 497

17/10/2020 16:16

exProf · Accepted Answer

Inizio col rispondere al tuo ultimo commento alla domanda
https://www.sosmatematica.it/forum/domande/modulo-velocita-iniziale/#post-12028
perché la risposta attiene anche a questa domanda e a tutte quelle in cui c'entri la gravità; la mia risposta a «tra i possibili risultati ci sono 38.468 e 38.362 m/s, il corretto è il secondo?» è «No, non è corretto nessuno dei due.»
Mi spiego.
In Italia c'è l'obbligo di legge [DPR 802/1982] di usare solo il valore standard SI
* g = 9.80665 = 196133/20000 m/s^2
in qualsiasi occasione pubblica, non 9.8 o 9.81 o ancor peggio 10; e la Scuola è un'istituzione pubblica. Ogni compito e/o interrogazione è un evento pubblico. Ogni insegnante è Pubblico Ufficiale, quindi con l'obbligo di far osservare le prescrizioni di legge.
Io insegnante non lo sono più, ma perché abbandonare le buone abitudini?
Probabilmente la fonte del tuo esercizio ha fatto i conti con un valore illegalmente approssimato: QUEL LIBRO NON SI SAREBBE DOVUTO ADOTTARE.
==============================
VENGO AL PROBLEMA (che si risolve senza il moto parabolico)
La parabola data
* y = - 4.9*x^2 + 6.0*x + 5.0 ≡
≡ y = 335/49 - (49/10)*(x - 30/49)^2 ≡
≡ y = - (49/10)*(x - 5*(6 - √134)/49)*(x - 5*(6 + √134)/49)
ha:
* asse di simmetria (x = 30/49) parallelo all'asse y;
* apertura (a = - 49/10) negativa, quindi concavità verso y < 0;
* vertice V(30/49, 335/49)
* zeri X(5*(6 ± √134)/49, 0)
---------------
Un punto materiale lanciato in modo da percorrere quella parabola tocca terra in
* X2(5*(6 + √134)/49, 0)
quindi alla distanza
* d = 5*(6 + √134)/49 ~= 1.79 m
dall'origine.
---------------
Se vuoi usare le leggi del moto, l'accelerazione di gravità ti serve.

exProf

(@exprof)

51551 punti

livello:

Genius I

12542 Risposte
34 6460 1663

17/10/2020 20:27

Anguus90 · Answer

[attach]5188[/attach] La situazione qui è molto più semplice, hai già esplicitata la traiettoria del moto, senza chiamare in gioco la legge oraria e la velocità, per trovare il punto in cui l'oggetto tocca terra, basta imporre che y, ossia la tua quota sia uguale a zero, a quel punto l'esercizio si riduce alla risoluzione di un'equazione di secondo grado

remanzini_rinaldo · Answer

y= -4,9x^2+6,0x+5,0 basta porre y = 0 4,9x^2-6x-5 = 0  x = (6+√6^2+98)/9,8 = (6+√134)/9,8 = 1,79 m

[Risolto] problema traiettoria

Domande