Un razzo sta accelerando in modo uniforme su una lunga rampa di lancio. Un osservatore misura la sua posizione ogni 0.2 s iniziando da quando il razzo passa da un punto di riferimento:
t=0s x(t)= 0m
t= 0.2s x(t)= 14 m
t= 0.4s x(t)= 31m
t=0.6s x(t)= 50 m
t= 0.8s x(t)= 71m
t= 10s x(t)= 95m
Come devo procedere? Grazie
824
punti
Livello 1
@chiarachiaretta : per fare che cosa? T'è rimasto il quesito nella tastiera, hai il click un po' frenetico.
@Sebastiano...ho trovato il testo in rete...bisogna trovare l'accelerazione del razzo in m/s^2
scusate il fastidio, ho dimenticato nella fretta e nell'ansia di segnare tutto.
QUESTO E' UN PROBLEMA MAL PROGETTATO E SCRITTO PEGGIO.
------------------------------
METODO BANALE
------------------------------
Le letture sono a intervalli costanti di un quinto di secondo e sono
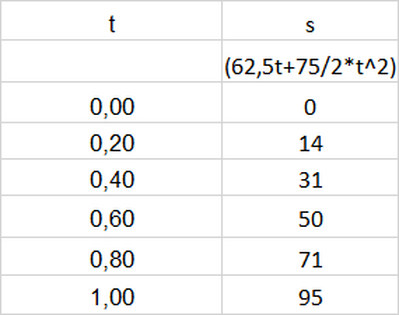
* X = {x} = {0, 14, 31, 50, 71, 95} m
le cui differenze prime sono
* X' = {Δx} = {14, 17, 19, 21, 24} m
da cui le velocità medie d'intervallo
* V = {v} = {Δx/Δt} = {14, 17, 19, 21, 24}/(1/5) = (70, 85, 95, 105, 120) m/s
le cui differenze prime sono
* V' = {Δv} = {15, 10, 10, 15}
da cui le accelerazioni medie d'intervallo
* A = {a} = {Δv/Δt} = {15, 10, 10, 15}/(1/5) = (75, 50, 50, 75) m/s^2
------------------------------
ALTERNATIVA SEMPLICE
------------------------------
Le letture sono a intervalli costanti di un quinto di secondo e sono
* X = {x} = {0, 14, 31, 50, 71, 95} m
le cui differenze seconde sono
* X'' = {Δ^2x} = {3, 2, 2, 3} m
da cui le accelerazioni medie d'intervallo
* A = {a} = {Δ^2x/Δt^2} = {3, 2, 2, 3}/(1/5)^2 = (75, 50, 50, 75) m/s^2
------------------------------
ALTERNATIVA ARZIGOGOLATA
------------------------------
La migliore interpolante polinomiale ai minimi quadrati delle coppie {t, x} date
* {{0, 0}, {1/5, 14}, {2/5, 31}, {3/5, 50}, {4/5, 71}, {1, 95}}
è un polinomio di grado quattro e non due
* x(t) = (5/24)*(125*t^4 - 250*t^3 + 295*t^2 + 286*t)
mentre dovrebb'essere
* x(t) = (a/2)*t^2 + V*t
---------------
Se questo fosse un problema serio applicherei una qualche ptocedura di ottimizzazione innescandola con
* (a, V) = ((5/24)*295, (5/24)*286) = (1475/24, 715/12) ~= {61.4583, 59.5833}
ma, per questo problema qui, è assai più ragionevole pensare che sia stato scritto sul tavolo di cucina con un po' di bambini intorno che facevano caciara.
51261
punti
Genius I
Ho provato a svolgerlo, ma l'accelerazione non è affatto uniforme, guardando le soluzioni proposte come alternativa, l'unica idea che mi viene in mente è quella che sia richiesta una media delle accelerazioni, in quel caso la risposta esatta sarebbe la d) 62,5 m/s^2 , ma ripeto, il problema per me è mal posto
3817
punti
Livello 4
95 = Vo+a/2 (1)
14 = 0,2Vo+a/2*0,2^2 = 0,2Vo+0,02a (2)
moltiplico ambo i membri della (2) per 5 allo scopo di ottenere Vo
70 = Vo+0,1a (3)
sottraggo la (3) dalla (1)
25 = 0,4a
a = 25/0,4 = 25*2,5 = 62,5 m/sec^2
Vo = 70-6,25 = 63,75 m/sec
verifica
96152
punti
Genius II
