Problema parabola

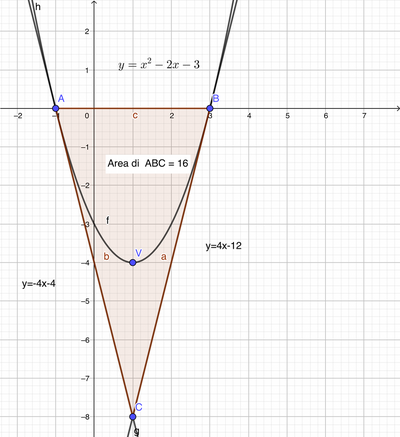
Determino il fascio di rette passati per il punto C:

Y+8= m*(x-1)

Metto a sistema l'equazione della parabola con il fascio di rette appena trovato e impongo la condizione di tangenza. Essendo il punto C esterno alla parabola (vedi grafico) troveremo due rette tangenti alla curva. 

{y+8= m*(x-1)

{y=x²-2x-3

Ricavando y dalla prima equazione e sostituendo nella seconda otteniamo 

X² - (m+2)*x + (m+5)=0

Imponendo la condizione di tangenza Delta = b²-4ac= 0 otteniamo:

m²+4m+4-4m-20=0 da cui m²-16=0, m=4 o m=-4

Sostituendo tali valori nel fascio di rette possiamo trovare le due rette tangenti alla parabola 

Y=4x-12  (m=4) 

Y=-4x-4  (m=-4)

Le intersezioni delle due rette con asse x, ottenute ponendo y=0 sono rispettivamente A(-1, 0) e B(3, 0)

Notiamo che il pto C ha ascissa 1 coincidente con l'ascissa del punto medio del segmento AB, base del nostro triangolo che quindi è isoscele. 

AB = 4

H=8

AREA = (8*4)/2 = 16

RIPASSI
------------------------------
L'area del triangolo che ha i vertici
* A ≡ P1(x1, y1), B ≡ P2(x2, y2), C ≡ P3(x3, y3)
è metà del valore assoluto di una semplice espressione delle coordinate
* S(ABC) = (1/2)*|x1*(y2 - y3) - x2*(y1 - y3) + x3*(y1 - y2)|
Se ABC sono allineati l'area del triangolo che li ha per vertici è zero.
------------------------------
La retta polare p(Γ, P) del punto P(u, v), il polo, rispetto alla cònica Γ si ottiene dall'equazione di Γ in forma normale canonica, f(x, y) = 0, lasciàndone inalterati i coefficienti e operando le sostituzioni (formule di sdoppiamento):
* x^2 → u*x; y^2 → v*y; x*y → (v*x + u*y)/2; x → (u + x)/2; y → (v + y)/2.
Se P è su Γ, p(Γ, P) è la tangente in P.
Se P è esterno a Γ, p(Γ, P) interseca Γ nei punti di tangenza delle tangenti condotte da P.
Se P è interno a Γ, p(Γ, P) non interessa il problema delle tangenti.
==============================
RISOLUZIONE
------------------------------
polo C(1, - 8)
conica Γ ≡ y = x^2 - 2*x - 3 ≡
≡ y = (x + 1)*(x - 3) ≡ x^2 - 2*x - y - 3 = 0
* polare p(Γ, C) ≡ 1*x - 2*(1 + x)/2 - (- 8 + y)/2 - 3 = 0 ≡
≡ y = 0
La polare è l'asse x, perciò i punti di tangenza sono gli zeri di Γ: A(- 1, 0) oppure B(3, 0). Quindi il triangolo ABC è isoscele sulla base AB lunga 4, di altezza |yC| = 8 e di area S(ABC) = 16.
Infine le tangenti sono le congiungenti
* CA ≡ y = - 4*(x + 1)
* CB ≡ y = 4*(x - 3)
Vedi
http://www.wolframalpha.com/input/?i=%5By%3D%28x%2B1%29*%28x-3%29%2Cy*%28y%2B4*%28x%2B1%29%29*%28y-4*%28x-3%29%29%3D0%5Dx%3D-2to5%2Cy%3D-9to2

Ciao di nuovo. Vedi allegato.