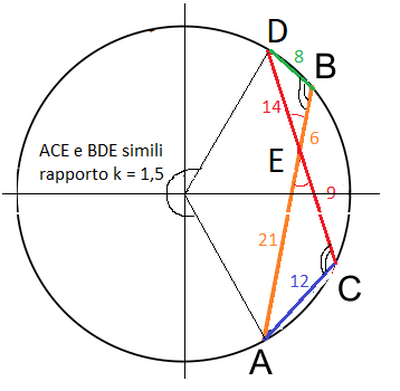
Buon pomeriggio a tutti; ecco il testo del problema n. 199 sul teorema delle corde dove sto incontrando difficoltà e per il quale chiedo il vostro prezioso aiuto: disegna una circonferenza e due corde : AB lunga 27 cm, e AC, lunga 12 cm. Una terza corda, CD, taglia AB nel punto E in modo che il segmento AE sia i 7/9 di AB e CE i 3/7 di AB. Determina il perimetro dei triangoli AEC e BED.
R. 42 cm; 28 cm. Ringrazio sin d'ora tutti coloro che vorranno rispondermi; chiedo, se possibile, la spiegazione di ciascun passaggio e il disegno della figura geometrica.