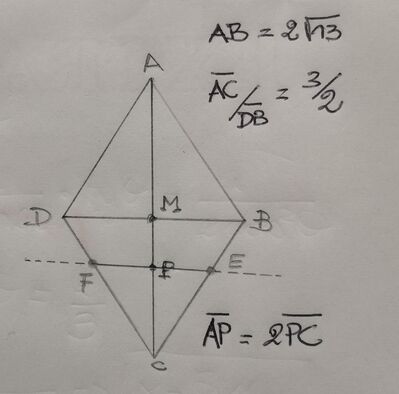
Un rombo $A B C D$, in cui il rapporto delle diagonali è $\frac{3}{2}$, ha perimetro $8 \sqrt{13} cm$.
a. Determina le lunghezze delle diagonali.
b. Sia $P$ il punto della diagonale maggiore $A C$ tale che $A P \cong 2 P C$. Traccia da $P$ la parallela alla diagonale $B D$, che interseca i lati $B C$ e $C D$ del rombo rispettivamente in $E$ e in $F$. Determina le aree delle due parti in cui il rombo resta diviso dal segmento $E F$.
$\left[\right.$ a. $8 cm , 12 cm ;$ b. $\left.\frac{32}{3} cm ^2 e \frac{112}{3} cm ^2\right]$