Sono date tre sferette $A, B$ e $C$ conduttrici identiche, tutte dotate di supporti isolanti.
All'inizio la sfera $A$ è elettrizzata con una carica positiva $Q,$ mentre le sfere $B$ e $C$ sono scariche. Poi $B$ è messa a contatto $\operatorname{con} A, C$ è posta in contatto $\operatorname{con} B$ e infine $C$ è messa in contatto ancora $\operatorname{con} A$.
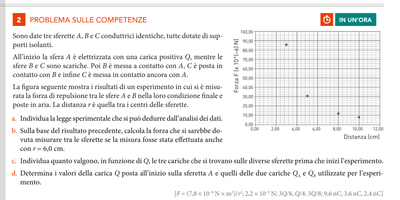
La figura seguente mostra i risultati di un esperimento in cui si è misurata la forza di repulsione tra le sfere $A$ e $B$ nella loro condizione finale $e$ poste in aria. La distanza $r$ è quella tra i centri delle sferette.
a. Individua la legge sperimentale che si può dedurre dall'analisi dei dati.
b. Sulla base del risultato precedente, calcola la forza che si sarebbe dovuta misurare tra le sferette se la misura fosse stata effettuata anche
$\operatorname{con} r=6,0 \mathrm{~cm}$
c. Individua quanto valgono, in funzione di $Q$, le tre cariche che si trovano sulle diverse sferette prima che inizil'esperimento.
d. Determina i valori della carica $Q$ posta all'inizio sulla sferetta $A$ e quelli delle due cariche $Q_{A}$ e $Q_{B}$ utilizzate per l'esperimento.
$$
\left[F=\left(7,8 \times 10^{-8} \mathrm{~N} \times \mathrm{m}^{2}\right) / r^{2} ; 2,2 \times 10^{-5} \mathrm{~N} ; 3 Q / 8, Q / 4 ; 3 Q / 8 ; 9,6 \mathrm{nC}, 3,6 \mathrm{nC}, 2,4 \mathrm{nCl}\right.
$$
Salve a tutti e grazie in anticipo per un eventuale aiuto, sto ormai provando da diverse ore a risolvere questo esercizio, nello specifico la prima consegna, ma invano.
Potreste mostrarmi l'esercizio svolto o guidarmi nello svolgimento?