[Risolto] Problema esponenziale come si risolve?

La legge esponenziale è fatta così: $N(t) = N_0 e^{kt}$ dove:
$N_0=$ numero iniziale di batteri
$k =$ coefficiente dell'esponente
$N(t)=$ funzione che, al variare del tempo, restituisce il numero di batteri.
$t=$ tempo, che supponiamo essere misura in ore (perché il problema ci dà solo dati relativi alle ore)

I dati forniti dal problema ci dicono che:

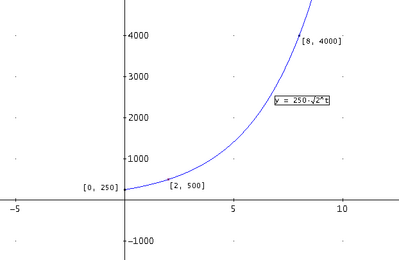
$t = 2$, $N(2)=500$
$t=8$, $N(8)=4000$

ma quando poniamo $t=2$ o $t=8$, l'espressione della formula esponenziale diventa

$N_0 e^{k2}$ e $N_0 e^{8k}$.

Queste informazioni ci permettono di scrivere il seguente sistema:

$\begin{cases} 500 = N_0e^{2k} \\ 4000 = N_0e^{8k} \end{cases} $

che è un sistema di due equazioni in due incognite, quindi possiamo risolverlo! Dalla prima, proviamo a ricavare $N_0$: $N_0 = \frac{500}{e^{2k}}$

sostituiamolo nella seconda: $4000 = \frac{500}{e^{2k}}e^{8k}$

$4000 = 500e^{8k-2k}$
$4000 = 500e^{6k}$
$\frac{4000}{500} = e^{6k}$

risolviamo la seguente equazione esponenziale passando ai logaritmi, secondo la formula $\log_a(b) = c $ se e solo se $ a^c = b$

$e^{6k} = 8 \ \rightarrow 6k = ln(8) \ \rightarrow  k = \frac{ln(8)}{6}$

Siamo pronti a trovare $N_0$, usando l'espressione che abbiamo ricavato prima:

$N_0 = \frac{500}{e^{2k}} = \frac{500}{e^{\frac{2}{6} \cdot ln(8)}$

Riscriviamo meglio l'esponenziale: ${e^{\frac{2}{6} \cdot ln(8)} = e^{\frac{1}{3}\cdot ln(8)}$

ma possiamo usare la proprietà delle potenze che dice $n\log_a(b) = \log_a(b^n)$ per portare $\frac13$ ad esponente di $8$, ottenendo
$e^{\frac{1}{3}\cdot ln(8)} = e^{ln(8^\frac{1}{3})} = e^{ln(\sqrt[3]{8})}= e^{ln(2)} = 2$

dove abbiamo usato il fatto che un esponente frazionario rappresenta una radice, quindi $8^\frac{1}{3} = \sqrt[3]{8}$ (che fa $2$) e la "proprietà" che dice che $a^{\log_a(b)} = b$. Quest'ultima non è proprio una proprietà, deriva dal fatto che esponente e logaritmo sono due funzioni una l'inversa dell'altra.

Siamo pronti per concludere: 

$N_0 = \frac{500}{e^{2k}}$ = $\frac{500}{e^{\frac{2}{6} \cdot ln(8)}$ = $\frac{500}{2} = 250$

Dai dati, sappiamo già che dopo $2$ ore diventano $500$, che è il doppio di $250$, quindi la risposta è: $2$ ore. 

Ciao,

dato che la cultura dei batteri ha una crescita esponenziale possiamo esprimere la loro crescita tramite la funzione

$n=n_{0}a^{t}$

Dove $n$ è Il numero dei batteri, $t$ il tempo , $n_{0}$ il numero di batteri iniziale e $a$ il fattore di crescita

Noi sappiamo che per $t=2h$ $n=500$ mentre per $t=8h$ $n=4000$

Sotiuendo i valori nella funzione:

$500=n_{0}a^{2}$ per cui $n_{0}=\frac{500}{a^{2}}$

$4000=n_{0}a^{8}$ per cui $n_{0}=\frac{4000}{a^{8}}$

Quindi:

$\frac{500}{a^{2}}=\frac{4000}{a^{8}}$

$a^6=8$ per cui $a^{2}=2$

Ora:

Sostituendo $a^{2}$ in $n_{0}=\frac{500}{a^{2}}$

$n_{0}=\frac{500}{2}=250$

Dato che sappiamo dai dati del problema che dopo $2h$ sarrano $500$ mentre abbiamo appena scoperto che inizialmente erano $250$, il tempo per raddopiare sarà $2h$

4000/500 = 8 = 2^k

ln8 = k*ln2 

k = ln8/ln2 = 3 ...in 6 ore (8-2)  i batteri sono raddoppiati 3 volte , pertanto in 2 ore sono raddoppiati una volta diventando 500 a partire dalla quantità iniziale ni

ni*2 = 500

ni = 500/2 = 250 

Domanda vecchiotta!

y = a·b^t con t>=0

è la funzione da determinare. Quindi bisogna calcolare a e b.

a=N° iniziale di batteri per t=0

{500 = a·b^2 passa per (2,500)

{4000 = a·b^8 passa per (8,4000)

Risolviamo per sostituzione:

a = 500/b^2

4000 = 500/b^2·b^8------------->b = - √2 ∨ b = √2 si scarta la radice negativa

a = 500/√2^2------->a = 250

Quindi inizialmente vi sono 250 batteri

Senza fare i calcoli possiamo subito dire che, in base ai dati del problema i batteri raddoppiano in 2 ore (la prima informazione del sistema!)

Verifica: y = 250·√2^t è la funzione di crescita

500 = 250·√2^t

LN(500) = LN(250·√2^t)

LN(500) = LN(250) + t·LN(√2)

t = (LN(500) - LN(250))/LN(√2)= LN(2)/LN(√2)=2 ore