Considera la funzione:
$$
f(x)= \begin{cases}x^{2}-(b+3) x+2 a+4, & \text { se } x \leq 3 \\ a \ln (x-2), & \text { se } x>3\end{cases}
$$
1. Determina per quali valori dei parametri $a$ e $b$ la funzione $f(x)$ è continua e derivabile in $x=3$.
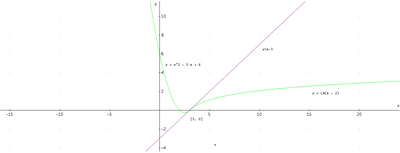
2. Nel punto precedente hai verificato che $a=1$ e $b=2$. Rappresenta graficamente la funzione $f(x)$, deducendo il grafico da quello delle funzioni elementari. Ricava l'equazione della retta tangente al grafico della funzione $f(x)$ in $x=3$.
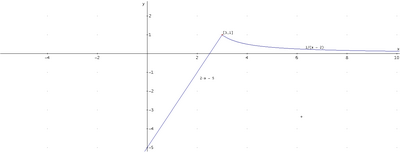
3. Disegna il grafico della funzione $f^{\prime}(x)$ e stabilisci se anch'essa è derivabile in $x=3$.
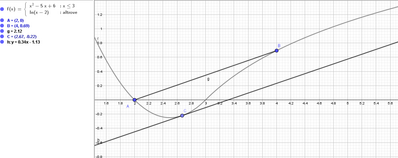
4. Dimostra che $f(x)$ soddisfa le ipotesi del teorema di Lagrange nell'intervallo $[2 ; 4]$ e determina l'ascissa del punto che ne soddisfa la tesi.
5. La regione di piano delimitata dal grafico della funzione $f(x)$ e dall'asse $x$ nell'intervallo $[0 ; 2]$ è la base di un solido le cui sezioni, con piani perpendicolari all'asse $x$, sono tutte dei quadrati. Calcola il volume del solido.
Mi servirebbero i punti 1 e 4