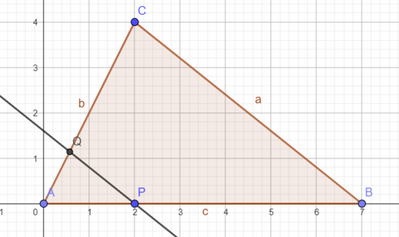
Sul lato $A B$ di un triangolo $A B C$ considera un punto $P$ tale che $A P \cong \frac{2}{5} P B$ e conduci per $P$ la parallela a $B C$ che interseca $A C$ in $Q$. Sapendo che $A C=28 cm$, determina il rapporto tra i perimetri e quello tra le aree dei triangoli $A P Q$ e $A B C$
$\left[\frac{2}{7} ; \frac{4}{49}\right]$
87
punti
Livello 1
I triangoli APQ e ABC sono simili (A in comune e gli angoli Q=C, P=B corrispondenti delle parallele QP//BC).
Essendo $AP= 2/5 PB$ avremo che:
$ AB = AP + PB = 2/5PB + PB = 7/5 PB$
e dunque:
$ AP = 2/5 PB = 2/5 (5/7 AB) = 2/7 AB$
Quindi il rapporto di similitudine è $k=2/7$.
Il rapporto tra i perimetri sarà proprio $k=2/7$, mentre quello tra le aree è $k^2 = 4/49$
Noemi
9382
punti
Livello 5
