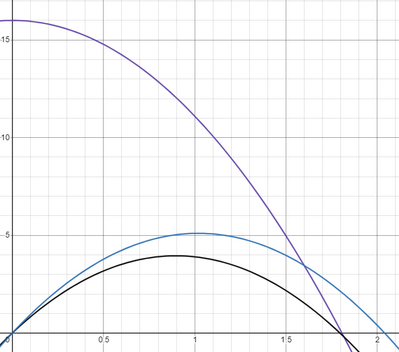
Massimo lascia cadere dal tetto di un edificio alto 16 m una pallina nello stesso istante in cui Adele al suolo , lancia verticalmente verso l'alto una seconda pallina , identica alla prima con velocita V0,A= 10 m/s . Trascura l'attrito con l'aria.
- In quale istante le due palline si trovano alla stessa distanza del suolo?
-Qual'è la velocità con cui Adele deve lanciare la pallina per fare in modo che questa si trovi affiancata all'altra alla minima altezza possibile?