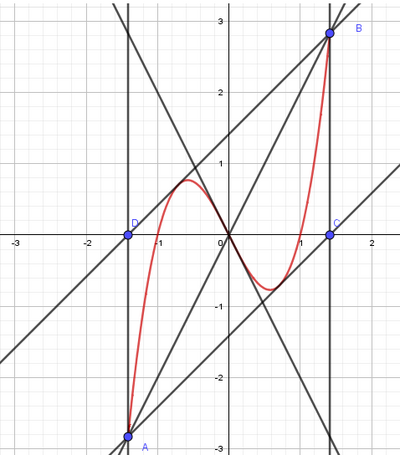
L'arco di curva $\gamma_{1}$ rappresentato in figura appartiene al grafico della funzione
$$
f(x)=a x\left(x^{2}-b\right) .
$$
$\gamma_{1}$ è inscritto nel parallelogramma $A B C D$. I lati $A D$ e $B C$ sono paralleli all'asse $y$, mentre $A B$ e $C D$ sono tangenti a $\gamma_{1}$ nei punti $P$ e $Q$, rispettivamente punti medi dei segmenti $B S$ e $D R$.
1. Ricava i valori dei parametri $a$ e $b$ usando i dati nel grafico e le ipotesi. Motiva il procedimento.
2. Dopo aver dimostrato che $a=2$ e $b=1$, considera la funzione $f(x)$ che trovi per questi valori dei parametri. Studia $f(x)$ nell'intervallo $[-\sqrt{2} ; \sqrt{2}]$.
Verifica che il grafico di $f(x)$ ha un punto di flesso nell'origine del sistema di riferimento. Determina l'equazione della retta $t$ tangente a $\gamma_{1}$ nell'origine e verifica che $t$ e la retta $A C$, diagonale del parallelogramma, si corrispondono in una simmetria rispetto all'asse delle ordinate.
3. Verifica che la funzione $f(x)$ soddisfa le ipotesi del teorema di Lagrange nell'intervallo $[-\sqrt{2} ; \sqrt{2}]$. Determina i punti dell'intervallo che soddisfano la tesi.