PENSO PROPRIO DI NO: non ci sono nozioni di algebra in quinta elementare.
Dovrebb'essere un procedimento per tentativi però non di calcolo, ma di riconoscimento su tavole precalcolate (dallo stesso scolaro di quinta elementare).
Domani sarò fuori Roma per l'intera giornata, ma per dopodomani ho già prenotato un libro di matematica della prima media; vi cercherò qualcosa di buono e, se l'avrò trovata, aggiornerò questa risposta.
PER ORA INVENTO A RUOTA LIBERA, coi programmi ministeriali sott'occhio
http://www.edscuola.it/archivio/norme/programmi/elementare.html#MATEMATICA
------------------------------
Nei programmi delle elementari ci sono
fra gli Obiettivi dello Scolaro
«Tradurre problemi elementari espressi con parole in rappresentazioni matematiche, scegliendo le operazioni adatte; quindi trovare le soluzioni e interpretare correttamente i risultati; inversamente, attribuire un significato a rappresentazioni matematiche date;»
«scrivere una successione di numeri naturali partendo da una regola data; viceversa, scoprire una regola che generi una data successione;»
fra le Motivazioni del Maestro
«In effetti, la conoscenza di tali algoritmi, insieme all'elaborazione di diverse procedure e strategie del calcolo mentale, contribuisce anche alla costruzione significativa della successione degli interi naturali e di altre importanti successioni numeriche (pari, dispari, multipli, ecc.)»
------------------------------
La bimba ideale (fra i figli dei miei nipoti (di zio) e dei miei figli le femminucce sono uno splendore [9 in greco, 10 in matematica, finale nazionale di ginnastica ritmica, ...], i maschietti andrebbero frustati [6 in latino, 5 in matematica, che noia la ginnastica, ...]) dovrebbe tradurre il problema di Giulio nella rappresentazione matematica di due successioni di naturali generate da due diverse regole; trovarne la soluzione come i due elementi corrispondenti dello stesso valore; interpretare correttamente il risultato come {lo stesso valore è l'età del padre; l'indice è l'età di Giulio}.
Le regole sono:
1) scrivi il quintuplo di ogni possibile età di Giulio;
2) scrivi la somma fra i cinque anni trascorsi e il decuplo dell'età che Giulio aveva cinque anni addietro, per le stesse età di Giulio per le quali hai scritto la successione dei quintupli.
------------------------------
Onestamente, se penso ai miei due nipoti (di nonno) non me li immagino a farsi un modello mentale di questo tipo. Devo telefonare a una scheggia di nipotina (di prozio) che fa la seconda media e sentire che mi dice.
Se mi dice cose interessanti, le aggiungo qui.
------------------------------
Rileggendo prima di pubblicare devo scusarmi per la chiacchiera, ma non mi va di riscrivere in meno di 400 parole: SCUSA LA CHIACCHIERA.
------------------------------
Aggiornamento di sabato 3 ottobre 2020, 15h 59'.
@Cenerentola
Ieri ho parlato con Claudia (prima media, 12 anni ad aprile): niente.
Oggi è venuto Federico (seconda media, 13 anni a marzo): niente.
Avrebbe dovuto portarmi il libro, ma se n'è dimenticato.
Non sono riuscito a parlare con Laura (scheggia bis).
Ho parlato solo per telefono con Valentina (la scheggia: terza media, 13 anni a dicembre) e la sua prima reazione è stata «Quant'hai detto che è, la differenza?»; le ho risposto che ho detto solo due rapporti, non la differenza e lei ha replicato «Lo devo vedere scritto. Quando torno a casa me lo scrivo e poi ti richiamo.»
Le interviste coi giovanissimi di famiglia non sono state un successo.
E' vagamente interessante solo il fatto che "la scheggia" abbia pensato subito alla differenza che, fra le due variabili, rimane costante. Ma non vedo come farne la base di un algoritmo, costruttivo o empirico che sia.
A questo punto mi arrendo e resto in attesa del prossimo quesito interessante.
==============================
SECONDO AGGIORNAMENTO di sabato 3 ottobre 2020, 20h 12'.
@Cenerentola
A sorpresa ho avuto il libro di Federico (da restituire domattina).
«L. Ferrando, L. Sasso "AL QUADRATO ARITMETICA 1" DeA SCUOLA | Petrini»
Da pag. 220 a pag. 223 c'è il meccanismo risolutivo specifico (che non è basato sui saperi delle elementari) ed è un metodo per lunghezze e colori.
A pag. 220 c'è un esplicito avviso che "Alle incognite molto spesso bisogna dare dei nomi, ossia dei simboli per identificarle, per esempio x, y ecc. oppure n ed m se si tratta di due numeri naturali, come nel problema dell'esempio precedente."
------------------------------
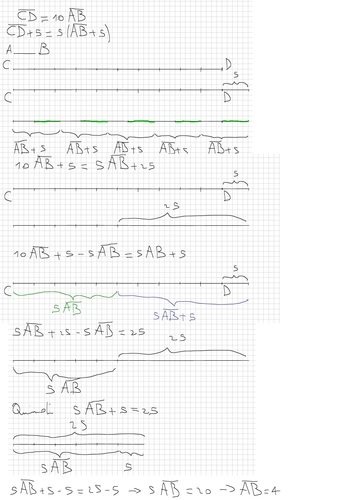
METODO RISOLUTIVO PER SEGMENTI (su carta a quadretti Q)
---------------
Sulla sinistra le etichette di riga, nel mezzo la situazione di cinque anni fa, sulla destra quella di oggi.
Nella prima riga le intestazioni incolonnate
* {Che cosa, Cinque anni fa, Oggi}
Nella seconda riga
* {Età di Giulio, un Q blu marcato con n, un Q blu e 5 rossi con n + 5}
Nella terza riga
* {Età del papà (5 anni fa), 10 Q blu con 10*n, 10 Q blu e 5 rossi con 10*n + 5}
Nella quarta riga
* {Età del papà (oggi), zona vuota, 5 Q blu e 25 rossi con 5*(n + 5)}
---------------
Sapendo che
* un Q rosso vale un anno
* un Q blu vale n anni
* 10 Q blu e 5 rossi valgono quanto 5 Q blu e 25 rossi
trovare il valore di n si fa con un secondo schema che realizza in righe successive, con quadretti colorati, la normale equazione lineare
* 10 Q blu e 5 rossi = 5 Q blu e 25 rossi ≡
≡ 5 Q blu = 20 rossi
e questo lo risolve anche un bambino di tre anni.
Il problema vero è: un bambino di undici anni ci arriva da solo fin qui?