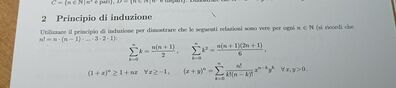Lo posso svolgere solo a rate.
Comincio a fare il n.3 e poi darò un'occhiata al n.4
(1 + x)^n >= 1 + nx
Per n = 1 vale l'uguaglianza per ogni x.
Sia vero per il generico n.
Passo di induzione
(1 + x)^(n+1) = (1 + x)^n * (1 + x ) >= (1 + nx) ( 1 + x) =
[ segue dall'ipotesi di induzione se 1 + x >= 0 => x >= -1 ]
= 1 + x + nx + nx^2 >= 1 + (n + 1 ) x
perché l'ultimo addendo é non negativo, e siamo arrivati.
Adesso svolgo il n.4 --- premetto per me sarà uno strazio, perché non so
scrivere in LaTeX.
( x + y )^n = S_k:0->n n!/[k! (n-k)! ] x^(n - k) y^k.
Per n = 1 é vero, (x + y )^1 = 1!/(0!1!) x^(1-0)y^0 + 1!/(1!0!) x^(1-1) y^1 =
= 1*x + 1*y = x + y
Sia vero per n generico
Passo di induzione
(x + y)^(n+1) = (x + y)*(x + y)^n = (x + y) * S_k:0->n n!/[k! (n-k)! ] x^(n - k) y^k =
= S_k:0->n n!/[k! (n-k)! ] x^(n - k + 1) y^k + S_k:0->n n!/[k! (n-k)! ] x^(n - k) y^(k+1)
Nella seconda somma poniamo m = k + 1 : m andrà da 1 a n + 1
e avremo
S_k:0->n n!/[k! (n-k)! ] x^(n - k+1) y^k + S_m:1->n+1 n!/[(m-1)!(n-m+1)!] x^(n+1-m) y^m =
= C(n,0) x^(n+1) + S_k:1->n [C(n, k) + C(n,k-1) ] x^(n-k+1) y^k + C(n,n) x^0 y^(n+1) =
= C(n+1,0) x^(n+1) + S_k:1->n n! ( 1/(k!(n-k)!) + 1/((k-1)!(n-k+1)!) ) x^(n+1-k) y^k +
+ C(n+1,n+1) y^(n+1) =
= C(n+1,0) x^(n+1) + S_k:1->n n! * [(n - k + 1 + k)/(k!(n+1-k)!) x^(n+1-k) y^k +
+ C(n+1,n+1) y^(n+1) =
= C(n+1,0) x^(n+1) + S_k:1->n (n+1)!/(k!(n+1-k)!) x^(n+1-k) y^k +
+ C(n+1,n+1) y^(n+1) =
= C(n+1,0) x^(n+1) + S_k:1->n C(n+1,k) x^(n+1-k) y^k + C(n+1,n+1) y^(n+1) =
= S_k:0-> n+1 C(n+1,k) x^(n+1-k) y^k
e la tesi é provata
Ho isolato da ogni somma il termine estremo il cui indice non é presente nell'altra
Ora passo al n. 1
S_k:1->n k = n(n+1)/2
Per n = 1 é vera : 1 = 1*(1+1)/2
Sia vera per n generico
Passo di induzione
S_k:1->n+1 k = S_k:1->n k + (n + 1) = n(n+1)/2 + (n+1) =
= (n+1) [n/2 + 1] = (n+1)(n+2)/2 = (n+1) * [(n+1) + 1]/2
e la tesi é provata.
Segui la stessa strategia per il n. 2 e dovresti trovare questo
per n = 1 é vero in quanto
1 = 1*(1+1)*(2+1)/6 = 1*2*3/6
Sia vera per il generico n;
il passo di induzione va avanti così
S_k:0->n+1 k^2 =
= S_k:1->n k^2 + (n + 1)^2 =
= n(n + 1)(2n + 1)/6 + (n + 1)^2 =
= (n + 1) [ n/6 * (2n + 1) + (n + 1 ) ] =
= (n+1) * [ 2n^2 + n + 6n + 6 ]/6 =
= (n + 1)/6 * (2n^2 + 7n + 6) =
= (n + 1)/6 *(2n^2 + 4n + 3n + 6) =
= (n + 1)*[2n(n + 2) + 3(n + 2)]/6 =
= (n + 1)(n + 2)(2n + 3)/6 =
= (n+1)[(n+1)+1][2(n+1) + 1]/6
e la tesi é provata.