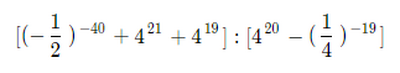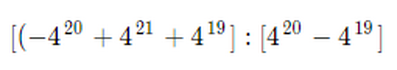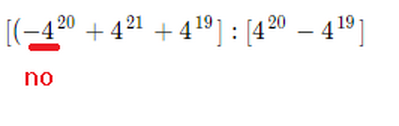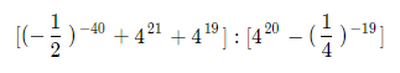Ciao a tutti, non riesco a capire questa espressione con potenze facente parte degli esercizi sulle proprietà distributive.
1) La proprietà distributiva della divisione non è applicabile al divisore
2) Posso comunque riscrivere tutto in base 4, ma non mi risolverebbe la questione
A parte calcolare i valori uno ad uno scomponendoli (che non volevo applicare), quali altre proprietà è possibile applicare per risolvere questa espressione?
Grazie mille!