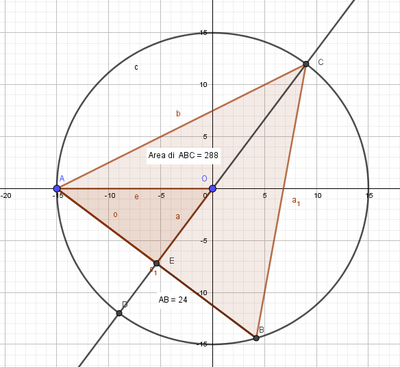
Il triangolo isoscele ABC, di base AB, è inscritto in una circonferenza di centro o e contiene o al suo interno. Sapendo che il raggio della circonferenza r è i 5/8 di AB e che la somma tra la metà di AB e 1/5 di r è 15 cm, determina l’area di ABC. Dovrebbe risultare 288cm2.. Grazie in anticipo