[Risolto] Iperbole

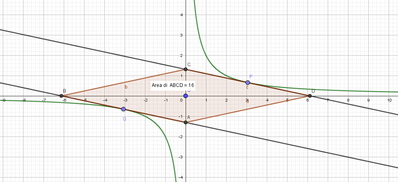
Se si considera il generico punto   (xo, 2/xo)

il fascio di rette che lo ha per centro ha equazione y - 2/xo = m (x - xo)

 

e - messo a sistema con l'equazione dell'iperbole - fornisce la risolvente

x [ mx - mxo + 2/xo ] - 2 = 0

m x^2 - (m xo - 2/xo) x - 2 = 0

D = 0 per avere la tangente

(m xo - 2/xo)^2 + 8m = 0

m^2 xo^2 + 4/xo^2 - 4m + 8m = 0

m^2 xo^2 + 4m + 4/xo^2 = 0

(m xo + 2/xo)^2 = 0

mxo = -2/xo

m = -2/xo^2

 

t) y = 2/xo - 2/xo^2 (x - xo) = - 2/xo^2  x + 4/xo

mentre nell'altro punto, x = - xo, si ha t'

y = - 2/xo^2  x - 4/xo

 

Da qui in poi dovrebbe essere semplice.

 

Le intersezioni con gli assi sono (0, 4/xo) e (2xo, 0)

e analogamente per l'altra retta, che darà

(0, -4/xo) e (-2xo, 0).

Si ottiene quindi un rombo ( lo lascio verificare a te )

le cui diagonali misurano 8/xo e 4xo

per cui S = 1/2 * 8/xo * 4 xo = 16.

Vale sempre 16

L'iperbole
* Γh ≡ x*y = 2
è riferita ai proprî asintoti e, poiché 2 > 0, ha i rami nei quadranti dispari.
Pertanto le tangenti in punti (P, Q) simmetrici rispetto all'origine devono
* intersecare entrambi gli asintoti/assi coordinati
* avere pendenza negativa
* avere equazioni, con a*b > 0,
** x/a^2 + y/b^2 = - 1
** x/a^2 + y/b^2 = + 1
quindi essere parallele, formando la parabola degenere
* Γp ≡ (x/a^2 + y/b^2)^2 = 1
------------------------------
I parametri si determinano imponendo la doppia tangenza
* Γh & Γp ≡ (x*y = 2) & ((x/a^2 + y/b^2)^2 = 1) & (a*b > 0) ≡
≡ (y = 2/x) & ((x/a^2 + (2/x)/b^2)^2 - 1 = 0) & (a*b > 0)
la risolvente
* (x/a^2 + (2/x)/b^2)^2 - 1 = 0
ha discriminante, da azzerare per la tangenza,
* Δ = 64*((a*b)^16)*((a*b)^2 - 8)^2 = 0 ≡ (a*b)^2 = 8 ≡
≡ b = √8/a
da cui
* Γh & Γp ≡ (x*y = 2) & ((x/a^2 + y/(√8/a)^2)^2 = 1) & (a*b > 0) ≡
≡ P(- a^2/2, - 4/a^2) oppure Q(a^2/2, 4/a^2)
------------------------------
Il quadrilatero di vertici
* A(- a^2, 0), B(0, - 8/a^2), C(a^2, 0), D(0, 8/a^2)
stante la simmetria quadrantale risulta essere un rombo di area S pari al semiprodotto delle diagonali
* S(ABCD) = (2*a^2)*(2*8/a^2)/2 = 16
che è un valore invariabile al variare di P.