[Risolto] Helppp

x^2 + y^2 = (2·√5)^2----> x^2 + y^2 = 20

[3, 0] è il fuoco dell'ellisse di equazione: x^2/a^2 + y^2/b^2 = 1

Quindi: a^2 > b^2 e c^2 = a^2 - b^2

Poniamo:  a^2 = α e b^2 = β

Quindi scriviamo il sistema:

{x^2/α + y^2/β = 1

{α - β = 3^2

cioè:

{2^2/α + (4/5·√21)^2/β = 1----> 4/α + 336/(25·β) = 1

{α - β = 9

La prima viene dal passaggio dell'ellisse per [2, 4/5·√21]

Quindi determiniamo le incognite α = β + 9

4/(β + 9) + 336/(25·β) - 1 = 0

Quindi arriviamo a scrivere: (16 - β)·(25·β + 189)/(25·β·(β + 9)) = 0

posto 25·β·(β + 9) ≠ 0---> β ≠ -9 ∧ β ≠ 0 (come deve essere per un'ellisse reale)

(16 - β)·(25·β + 189) = 0-----> β = - 189/25 ∨ β = 16

(la prima si scarta)

α = 16 + 9----> α = 25

Equazione ellisse: x^2/25 + y^2/16 = 1

che messa a sistema con la circonferenza determina le eventuali intersezioni:

{x^2/25 + y^2/16 = 1

{x^2 + y^2 = 20

Dalla seconda: y^2 = 20 - x^2

x^2/25 + (20 - x^2)/16 = 1

x^2/25 + (20 - x^2)/16 - 1 = 0

Sviluppando si ottiene: 1/4 - 9·x^2/400 = 0

Risolta fornisce: x = - 10/3 ∨ x = 10/3

Quindi:

y^2 = 20 - (10/3)^2----> y^2 = 80/9 per cui

y = - 4·√5/3 ∨ y = 4·√5/3

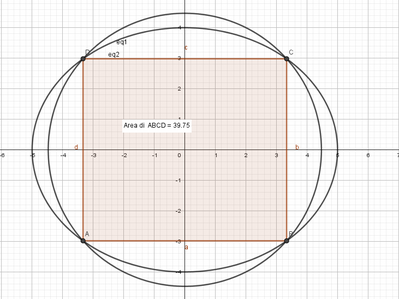
I quattro punti sono:

A [- 10/3, - 4·√5/3]

B [ 10/3, - 4·√5/3]

C[10/3, 4·√5/3]

D [- 10/3, 4·√5/3]

Sfruttando la doppia simmetria del problema determiniamo l'area del quadrilatero tramite le coordinate di C:

Α = 4·(10/3)·(4·√5/3)---> Α = 160·√5/9 = 39.75 circa