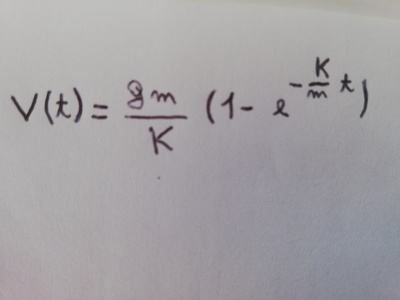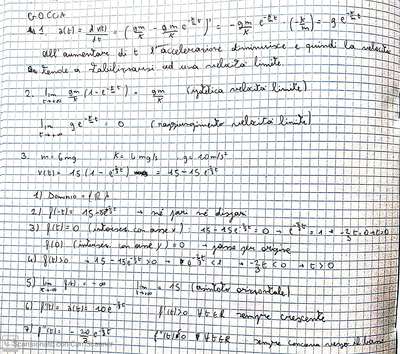L’accelerazione si studia come derivata della velocità, quindi per prima cosa devi derivare quella funzione (ovviamente al posto della solita x qui abbiamo la t come variabile)
〖a(t)=v〗^' (t)=gm/k∙(k/m e^(-k/m t) )=ge^(-k/m t)
Si può notare subito come l’accelerazione sia una quantità sempre positiva (un esponenziale del tipo ex è sempre positivo). Inoltre, all’instante t=0 l’accelerazione è uguale a g, mentre per t che tende all’infinito l’accelerazione tende a zero.
Ciò significa che la gocciolina d’acqua accelera sempre meno fino a stabilizzarsi ad una velocità costante (dove appunto a=0).
Per dimostrare questa caratteristica puoi anche fare la derivata prima dell’accelerazione (cioè la derivata seconda della velocità):
a^' (t)= -gk/m e^(-k/m t)
Che infatti è una quantità sempre negativa (= l’accelerazione decresce fino ad annullarsi).
lim┬(t→∞)〖v(t)=〗 gm/k
lim┬(t→∞)〖a(t)=0〗
Questi limiti confermano quanto detto prima: per t che tende all’infinito la velocità diventa costante (gm/k) e ciò significa che l’accelerazione tende a zero.
Per tracciare il grafico dovrai studiare queste parti:
Dominio: tutto R (essendo t il tempo, probabilmente il grafico intende t>0)
Simmetrie: non ci sono perché la funzione non è né pari né dispari.
Intersezioni: il grafico passa per l’origine (se t=0, allora v=0)
Segno: Ti basta studiare il segno della parentesi, quindi vedere quando quell’esponenziale è minore di 1. Facendo il logaritmo ottieni -kt/m <0 , cioè t>0.
In questo modo vediamo che la funzione è sempre positiva visto che consideriamo solo t>0
Limiti: abbiamo già visto che per t che tende all’infinito abbiamo v = gm/k, quindi la funzione presenta un asintoto orizzontale.
Derivata prima: sarebbe l’accelerazione, quindi sappiamo già che è sempre positiva e quindi la funzione non presenta né massimi né minimi (abbiamo però una funzione crescente).
Derivata seconda: anche questa l’abbiamo già calcolata e abbiamo visto che è sempre negativa, quindi nessun flesso ma abbiamo una funzione con concavità rivolta verso il basso:
Per il grafico disegnato (che non so come mostrarti) penso tu possa cercarlo online o con photomat.
Il teorema degli zeri afferma che, se una funzione f(x) è continua in un intervallo chiuso [a;b] e in più si ha che il segno di f(a) è diverso dal segno di f(b), allora all’interno di [a;b] la funzione f(x) presenta sicuramente almeno uno zero.
Per mostrare che la nostra funzione ha un solo zero basta far notare che se t>0 la velocità è sempre positiva, mentre se si considera un t<0 la velocità è sempre negativa. Di conseguenza l’unica volta in cui la velocità si annulla è in t=0.
Qui si tratta semplicemente di risolvere un integrale, facendo attenzione che se x (finora chiamata t) è negativa, allora la velocità è negativa. Quindi tra x=-1 e x=0 è necessario spezzare l’integrale e cambiarlo di segno:
∫_(-1)^4▒〖v(t)dt= -∫_(-1)^0▒〖v(t)dt+ ∫_0^4▒v(t)dt〗〗
Calcoliamo prima l’integrale indefinito:
∫▒〖gm/k-gm/k e^(-k/m t) 〗 dt= gm/k t+ (gm^2)/k^2 e^(-k/m t)+c
Ora basta sostituire a t gli estremi degli integrali e sottrarre tra loro i risultati:
∫_(-1)^0▒〖v(t)dt= (gm^2)/k^2 +〗 gm/k- (gm^2)/k^2 e^(k/m)
∫_0^4▒〖v(t)dt=4gm/k+ (gm^2)/k^2 e^(-4k/m)-(gm^2)/k^2 〗
Ora non ti resta che fare la differenza tra i due integrali ed il gioco è fatto!