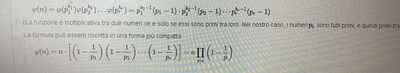Qualcuno che mi mostra i passaggi
$$
\varphi(n)=\varphi\left(p_{1}^{k_{1}}\right) \varphi\left(p_{2}^{k_{2}}\right) \ldots \varphi\left(p_{r}^{k_{r}}\right)=p_{1}^{k_{1}-1}\left(p_{1}-1\right) \cdot p_{2}^{k_{2}-1}\left(p_{2}-1\right) \cdots p_{r}^{k_{r}-1}\left(p_{r}-1\right)
$$
(La funzione è moltiplicativa tra due numeri se e solo se essi sono primi tra loro. Nel nostro caso, i numeri $p_{i}$ sono tutti primi, e quindi primi tra
La formula può essere riscritta in una forma più compatta:
$$
\varphi(n)=n \cdot\left[\left(1-\frac{1}{p_{1}}\right)\left(1-\frac{1}{p_{2}}\right) \cdots\left(1-\frac{1}{p_{r}}\right)\right]=n \prod_{p \mid n}\left(1-\frac{1}{p}\right)
$$
per arrivare alla forma compatta( argomento funzione di eulero)