Esercizio sulle parabole

Question

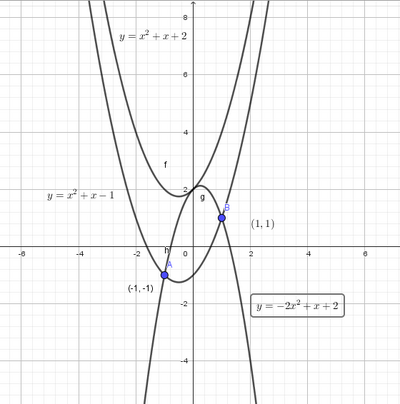
Passa per A(-1 ;-1)$ e per B(1 ; 1)$ ed è tangente alla parabola di equazione y=x^2+x+2$. Ciao. Premetto di aver risolto l'esercizio e di trovarmi (in parte) con il risultato. [attach]40996[/attach] Ho prima messo a sistema la parabola generica e quella che mi fornisce il problema ottenendo (a-1)x^2+(b-1)x+c-2=0. Ho poi impostato il delta = 0 poichè le due parabole sono tangenti. Ho poi scritto le tre condizioni (delta e passaggio per i punti A e B) per trovare a, b e c della parabola in un nuovo sistema. -1=a-b+c; 1=a+b+c (b-1)^2-4(a-1)(c-2)=0. Ho ottenuto però due soluzioni (a=1, b=1 e c=-1 e poi a=-2, b=1 e c=2) e quindi due parabole differenti. L'esercizio mi riporta solo una delle due e non capisco come mai non consideri l'altra. Tra l'altro, è possibile risolvere diversamente il problema? Magari tramite i fasci di parabola? L'esercizio si trova sotto l'argomento fasci. Attendo un riscontro. Grazie.

exProf · Accepted Answer

Per definizione due curve, y = f(x) e y = g(x), sono tangenti nel punto T(k, m) se e solo se T è un punto comune (f(k) = g(k) = m) e in esso hanno la medesima retta tangente (f'(k) = g'(k)).
------------------------------
L'esercizio 396 manca della consegna, che è la frase in testa al gruppo di esercizi, e che con ogni probabilità deve chiedere di "determinare la parabola che" oppure "determinare la parabola con asse PARALLELO ALL'ASSE (x | y) che" soddisfà alle condizioni espresse nei seguenti esercizi.
Nel secondo caso il problema è piuttosto semplice, nel primo un po' meno.
Il risultato atteso suggerisce che si tratti di determinare la parabola con asse parallelo all'asse y, quindi con equazione della forma
* Γ ≡ y = h + a*(x - w)^2
con pendenza
* m(x) = 2*a*(x - w)
specificate in funzione di
* apertura a != 0
* vertice V(w, h)
---------------
Il sistema dei vincoli imposti dalle condizioni d'appartenenza di A(- 1, - 1) e di B(1, 1)
* (- 1 = h + a*(- 1 - w)^2) & (1 = h + a*(1 - w)^2) ≡
≡ (w = - 1/(2*a)) & (h = - (4a^2 + 1)/(4*a))
da cui
* Γ(a) ≡ y = a*(x + 1/(2*a))^2 - (4a^2 + 1)/(4*a)
* m(x) = 2*a*(x + 1/(2*a))
determina le coordinate del vertice in funzione dell'apertura, che resta il solo parametro da determinare in base alla condizione di tangenza con la parabola data
* γ ≡ y = x^2 + x + 2
che ha pendenza
* m1(x) = 2*x + 1
---------------
* (f(k) = g(k) = m) & (f'(k) = g'(k)) ≡
≡ (a*(x + 1/(2*a))^2 - (4a^2 + 1)/(4*a) = x^2 + x + 2 = y) & (2*a*(x + 1/(2*a)) = 2*x + 1) ≡
≡ (a = - 2) & (x = 0) & (y = 2)
da cui
* T(0, 2)
* Γ(- 2) ≡ y = - 2*x^2 + x + 2
che sembra proprio (sbirciando la pagina curva) il risultato atteso ed è unico, non doppio.
La tua procedura di calcolo ha introdotto una soluzione spuria, credo perché l'equazione risolvente del sistema fra due parabole non è la stessa di quello fra una parabola e una retta.

exProf

(@exprof)

51564 punti

livello:

Genius I

12551 Risposte
34 6469 1663

27/03/2023 11:14

LucianoP · Answer

@anna-sa91 L'altra parabola che hai trovato differisce da quella data unicamente dal termine noto: risulterà quindi tangente a quella data non al finito, ma all'infinito. [attach]41007[/attach]

[Risolto] Esercizio sulle parabole

Domande