Buonasera,
qualcuno sarebbe in grado di spiegarmi lo svolgimento di questo esercizio.
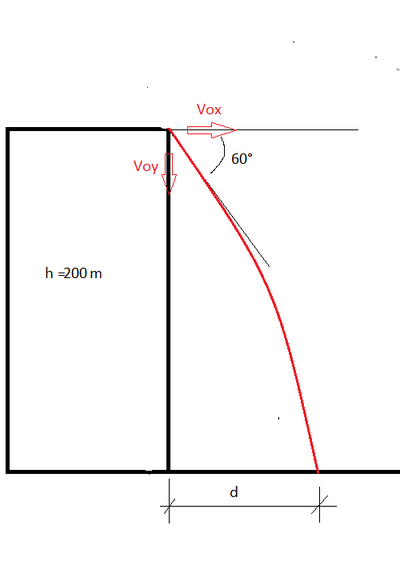
Un oggetto viene lanciato da un'altezza di 200 m verso il basso con un'inclinazione di 60° rispetto all'orizzontale e con velocità iniziale di 30,0 m/s. A quale distanza orizzontale l'oggetto raggiunge il suolo?