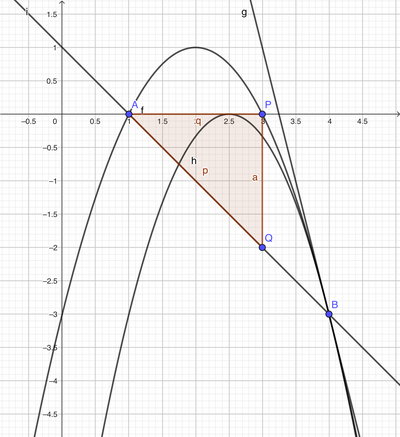
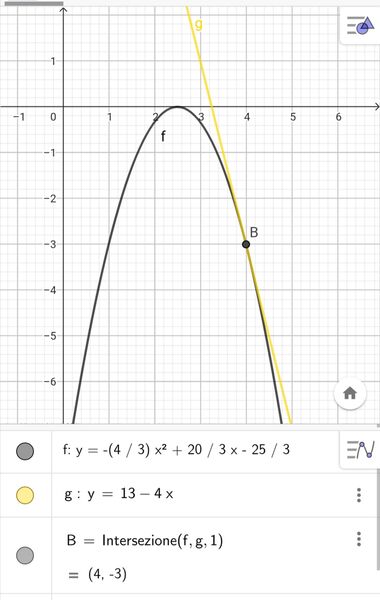
a. Scrivi l'equazione della parabola con asse parallelo all'asse $y$, passante per $A(1 ; 0), B(4 ;-3)$ e tangente in quest'ultimo punto alla retta $t$ di coefficiente angolare $-4$.
b. Per un punto $P$ dell'arco $A B$ di parabola, conduci la retta parallela all'asse $y$ e indica con $Q$ il punto che tale retta ha in comune con la corda $A B$. Determina $P$ e $Q$ in modo che l'area del triangolo $A P Q$ sia 2.
c. Scrivi l'equazione del fascio di parabole tangenti in $B$ alla retta $t$ e trova quale di queste ha il vertice sullase delle $x$.
$\left[\right.$ a) $y=-x^2+4 x-3 ;$ b) $P(3 ; 0), Q(3 ;-2)$; c) $\left.y=-\frac{4}{3} x^2+\frac{20}{3} x-\frac{25}{3}\right]$
Il punto A mi è venuto quindi potete anche non ripeterne lo svolgimento, mentre per il punto B vi spiego il mio tentativo (che non ha funzionato e non so perché)
Ho calcolato la retta ab y=-x+1, ho scritto che la base del triangolo era rad2(k-1) e l'altezza l'ho calcolato facendo distanza punto retta con Q (k, k-1).
Per il punto c non so proprio come fare